The focus of this research lies in the study of complex particle suspensions, with an emphasis on elucidating the intricate relationships between their microstructural attributes – such as the rheology of the suspending medium and/or microscopic inter-particle interactions – and the consequential macroscopic flow responses encompassing viscosity, normal stresses, and relaxation times. To achieve this objective, the precise numerical prediction of the dynamics and mechanical properties of micro/nano-particle suspensions under the influence of both simple and complex suspending media, as well as intricate micro-flow conditions, stands as a pivotal requirement. In recent years, we have developed a highly efficient mesoscopic particle simulation platform based on the Smoothed Dissipative Particle Dynamics (SDPD) and Smoothed Particle Hydrodynamics (SPH) techniques [1]. This platform enables us to analyze accurately the thermal and rheological properties of complex multiphase particulate systems.
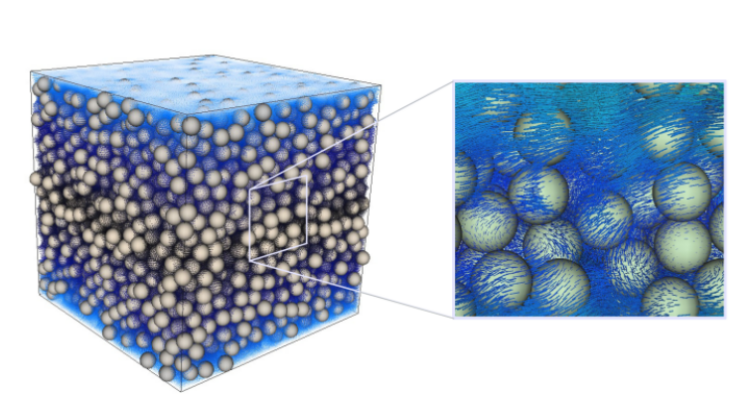
Particles suspended in complex media
Building upon validated SPH-SDPD schemes for colloidal and non-colloidal suspensions in Newtonian fluids [2,3,4,5,6], we have formulated a novel model specifically tailored to particles immersed in non-Newtonian viscoelastic media akin to Maxwell-type fluids [7,8] (Fig. 1). As an illustrative application, this model has been instrumental in analyzing the so-called “viscoelastic shear-thickening” reported in suspensions employing highly elastic Boger matrices under steady shear, yielding results in close accordance with experimental observations [9] (Fig.2).
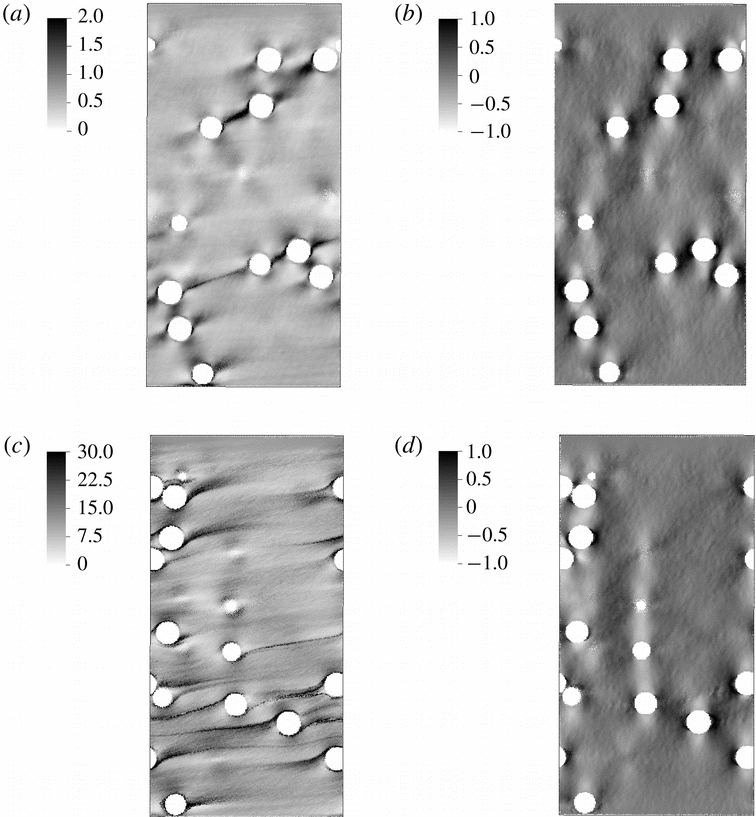
Fig. 1: Particle distribution in the shear plane at different Deborah numbers (top: De=0.5 – bottom: De=2.0). Left: polymer elongation field Tr[c]; Right: viscoelastic dissipation field.

Fig. 2: Left: Relative suspension viscosity. Viscoelastic shear-thickening at 30% solid volume fraction: comparison SPH vs different experimental systems with Boger matrices. Right: polymer elongation field (3D simulation) [9].
Reduced order models: lubrication dynamics
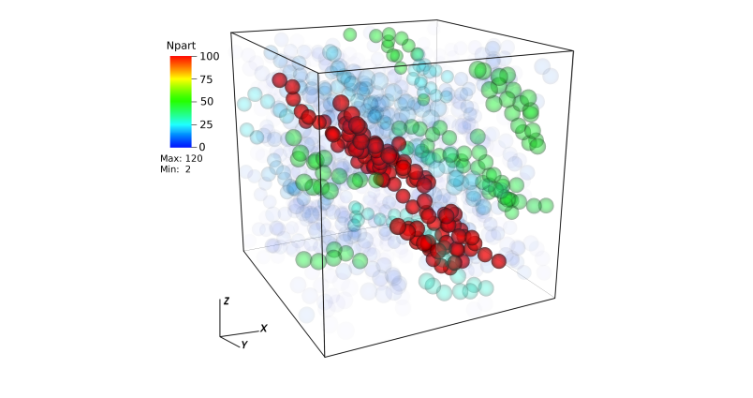
More recently, our research has shifted towards the development of reduced-order models for dense suspensions, obviating the need for an explicit representation of the liquid phase. This is accomplished by introducing properly defined short-range pairwise lubrication forces acting between suspended particles (Fig. 3). Nevertheless, simulating nearly-contacting solid particles within suspensions poses a formidable challenge due to the divergent nature of short-range lubrication forces. This limitation, related to explicit integration schemes, has been mitigated through the introduction of a novel semi-implicit splitting integration method for lubrication, as detailed in [10,11]. This innovative approach circumvents the resource-intensive full matrix inversion by formulating a series of manageable linear systems solvable analytically, thus significantly reducing CPU time requirements for simulating accurately dense systems (Fig. 4).
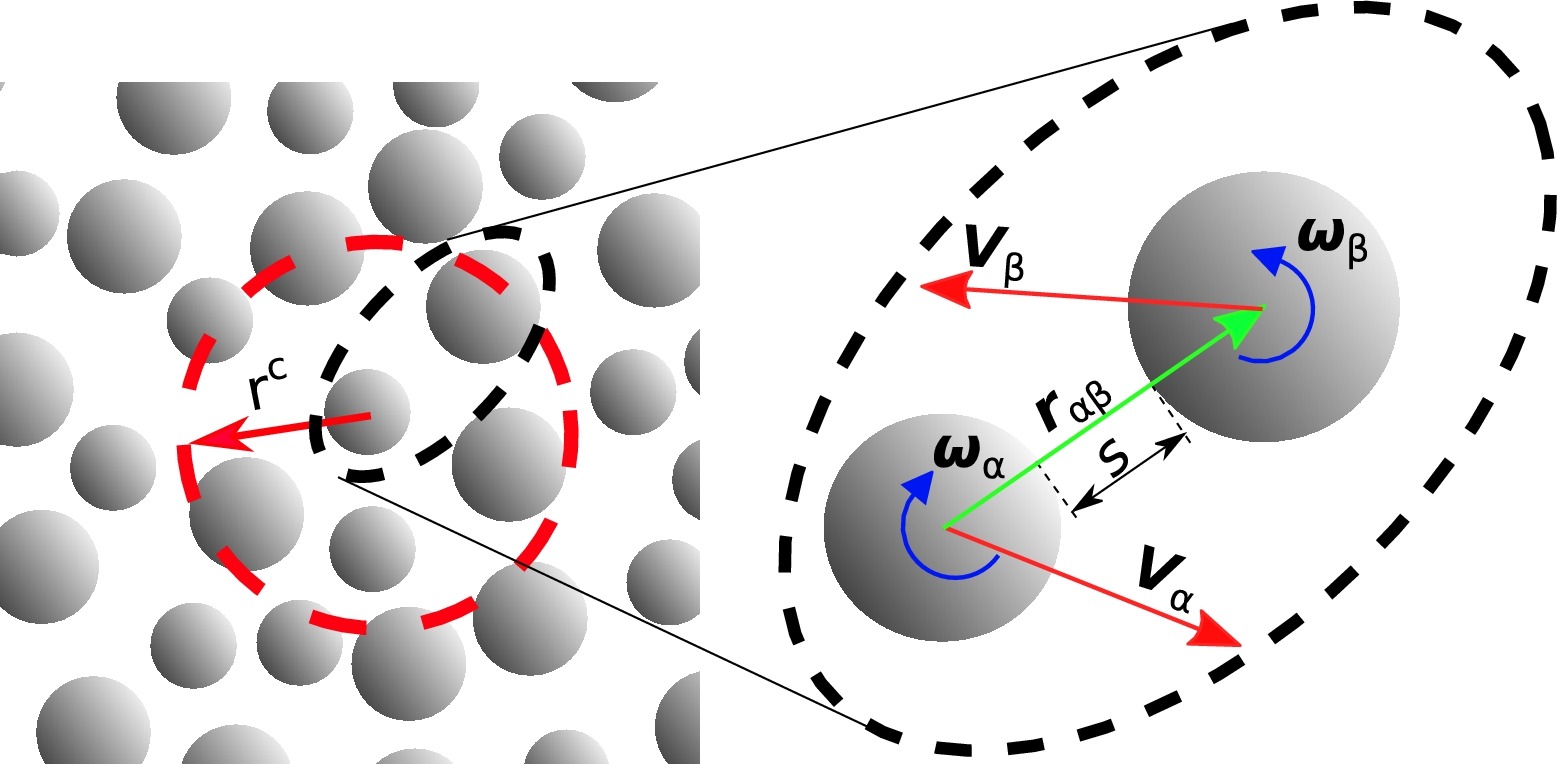
Fig. 3: Schematics of suspended solid particles in a Newtonian fluid under lubrication pairwise interaction. Solvent liquid is implicitly modelled trough short-range lubrication.
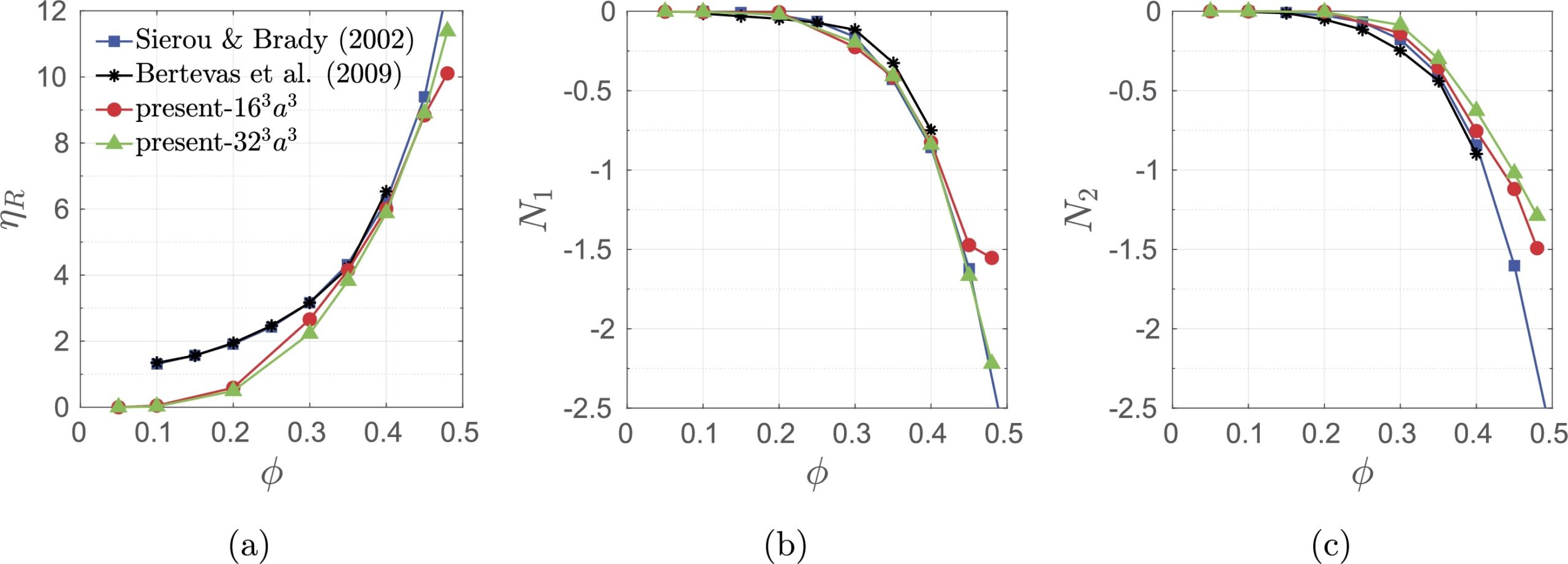
Fig. 4: Rheological validation under steady shear flow. Viscometric functions obtained in the Lubrication Dynamics model vs fully-resolved Stokesian Dynamics simulations results. Results are accurate for dense systems at solid volume fractions Φ> 0.3 [11].
Modified lubrication models
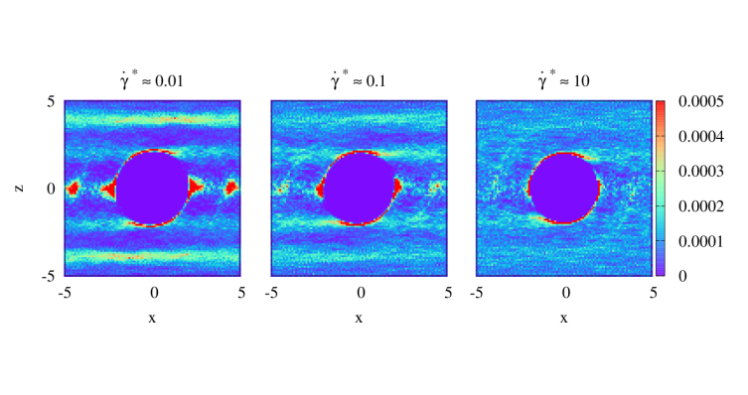
Furthermore, these techniques are adaptable to investigate dense suspensions within complex fluids by incorporating non-Newtonian generalizations for shear thinning/thickening media using biviscous models [12,13]. The modified lubrication models can also accommodate hidden high-shear non-Newtonian effects of the liquid medium [14,15] or particle surface slip [16], and provide two possible routes to explain the puzzling “shear-thinning” behavior reported in experiments of non-Brownian suspensions with Newtonian media [14] (Fig. 5). The modified lubrication models allow also to simulate with a minimal number computational degrees other complex systems such dense particulates immersed in pseudo-yield stress fluids [17].
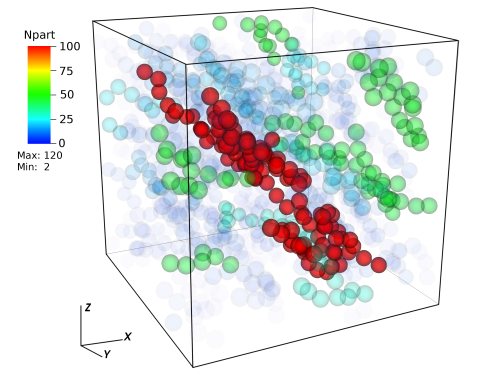
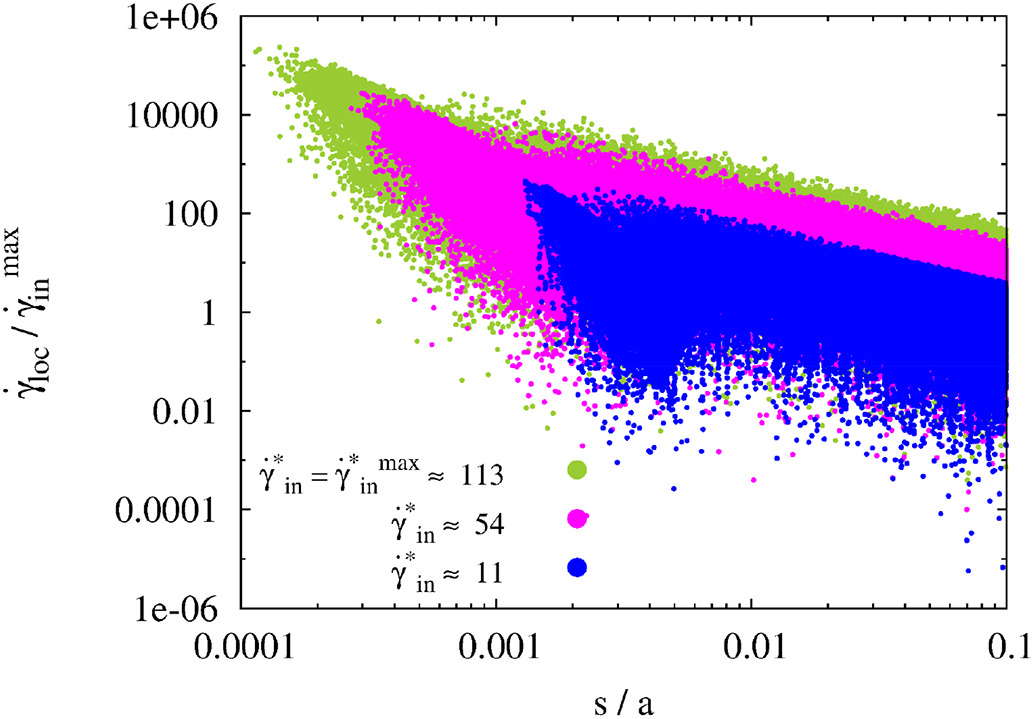
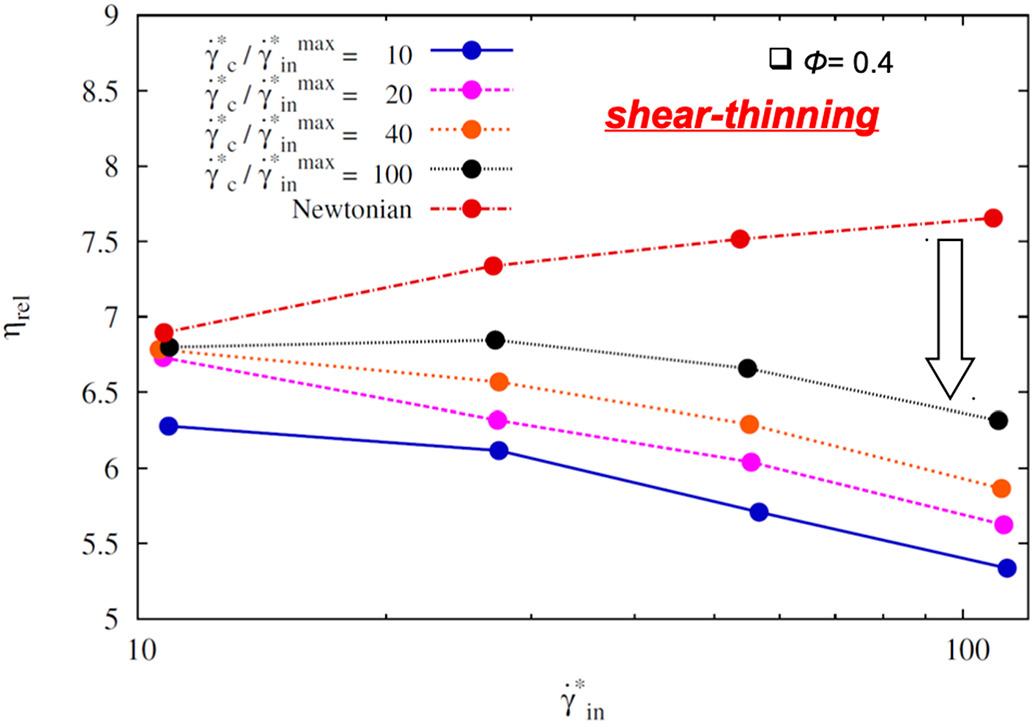
Fig. 5: Left: anisotropic suspension microstructure under shear. Center: Distribution of shear-rates in the gaps between nearly-touching particles. Due to the strongly anisotropic microstructure, local values of the shear rates in the particle gaps can be order of magnitude larger than the macroscopic one, thus allowing the liquid to locally access weak non-Newtonian effects, even for nominally-Newtonian suspending media (e.g. low MW silicon oils). Right: This can ultimately lead to shear-thinning of the whole suspension [14].
Frictional suspension and tribology
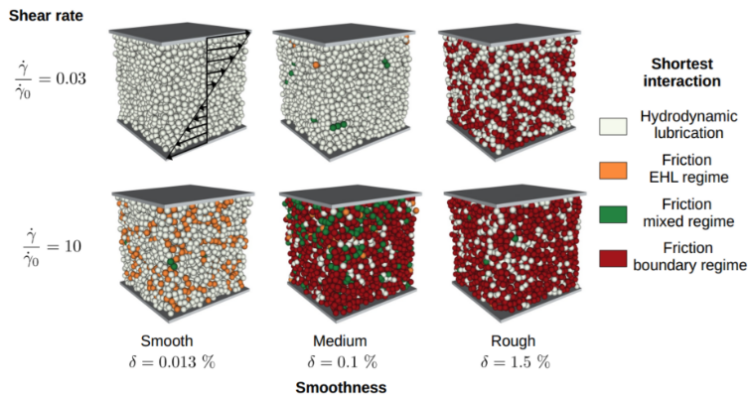
Recently, our research has further ventured into the study of frictional particles featuring tribologically-variable friction coefficients [18]. In this context, particle roughness-dependent frictional forces have been introduced following Stribeck curves encompassing boundary, mixed, and full-film lubricated regimes (Fig. 6). It was shown that particle roughness is the key factor in defining specific families of Stribeck curves, bridging the gap between the observed Newtonian, Continuous Shear Thickening (CST), and Discontinuous Shear Thickening (DST) behaviors prevalent in real-world systems.
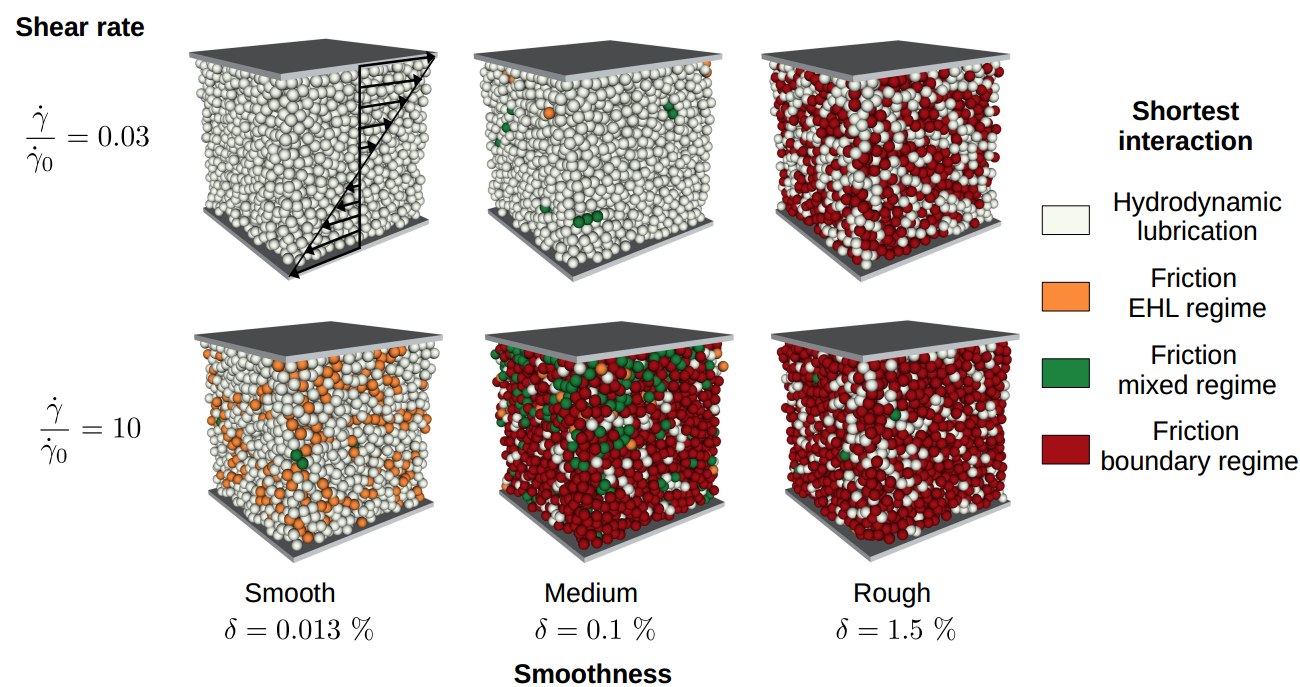
Fig. 6: Distribution of particles in frictional contacts (boundary, mixed or elasto-hydrodynamic lubrication regimes) as well as under pure hydrodynamic lubrication interactions. The distribution of contacts depends strongly on particle roughness (as well as the interparticle load and solvent viscosity) and can lead to Newtonian, CST or DST responses [18].
Dynamics and rheology of self-assembling magnetic chains
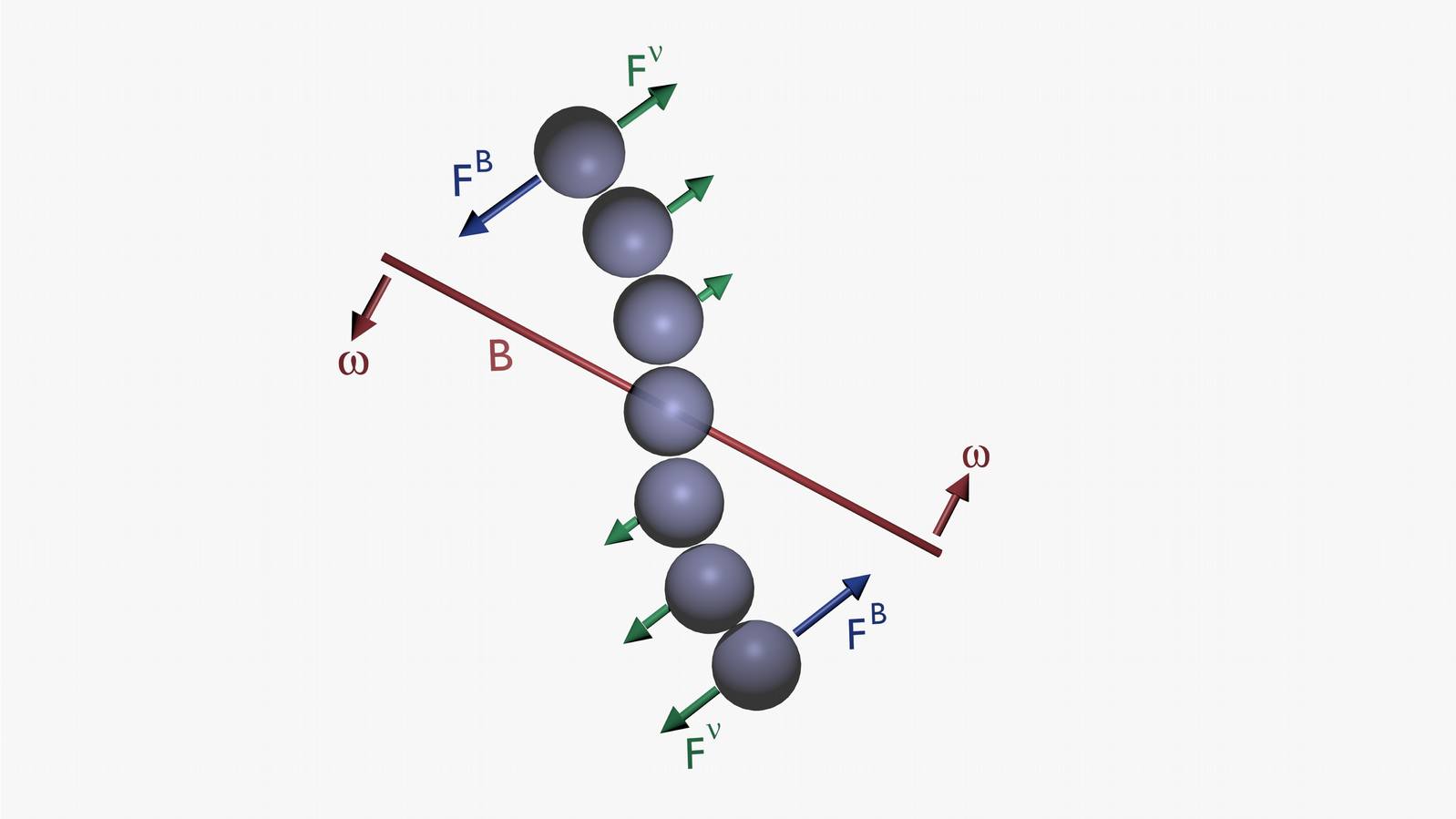
Superparamagnetic microbeads have been proven to enable manipulation in microfluidic systems and lab-on-a-chip applications by enhancing a number of operations including mixing, separation, and labelling. In a constant external magnetic field B, they align forming long chains. Such a kind of aggregation is limited when the magnetic field is rotating, i.e. there is a competition between magnetic and viscous forces, which determines the dynamics of the system (Fig. 7).
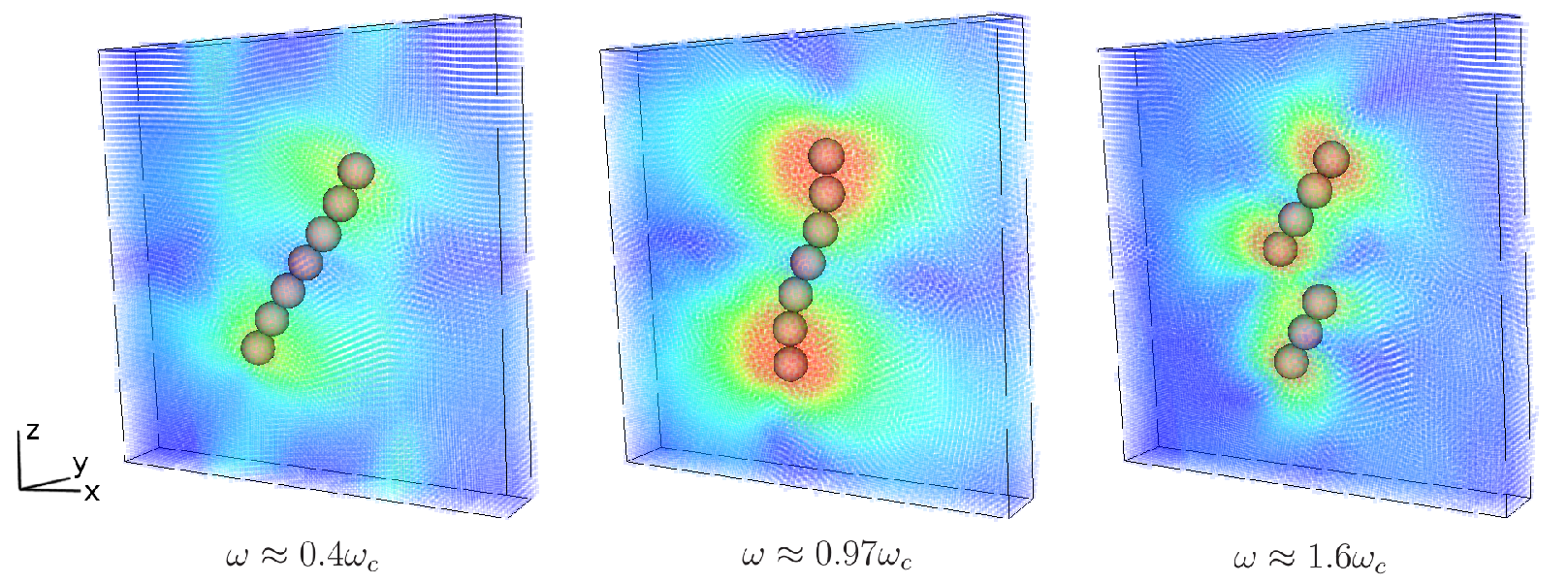
Fig 7: Dynamics of a superparamagnetic chain interacting with an external rotating field B. Left: B-frequency below the critical frequency – rigid-body chain’s rotation. Middle: close to critical frequency – S-shape rotation. Right: above critical frequency: chain’s breakup.
From experimental observations, the chains under a rotating magnetic field show a typical S-shape and, if the frequency is high enough, they will eventually break up into smaller fragments in order to reduce their viscous drag (fig. 7). The critical frequency which determines the rupture of the chain depends on the frequency of rotation, viscosity, and magnetization. In [19] a new lubrication-based model of linear magnetic chain was presented, which is able to predict analytically the critical frequency of instability and its general rotating dynamics. The incorporation of lubrication effects allows us to understand qualitatively the morphology of the chain and to predict its breakup quantitatively. Comparison of the current model with existing models and numerical results using Smoothed Particle Hydrodynamics is showed in Fig. 8 (left) where experimental data are shown on fig.8 (right).
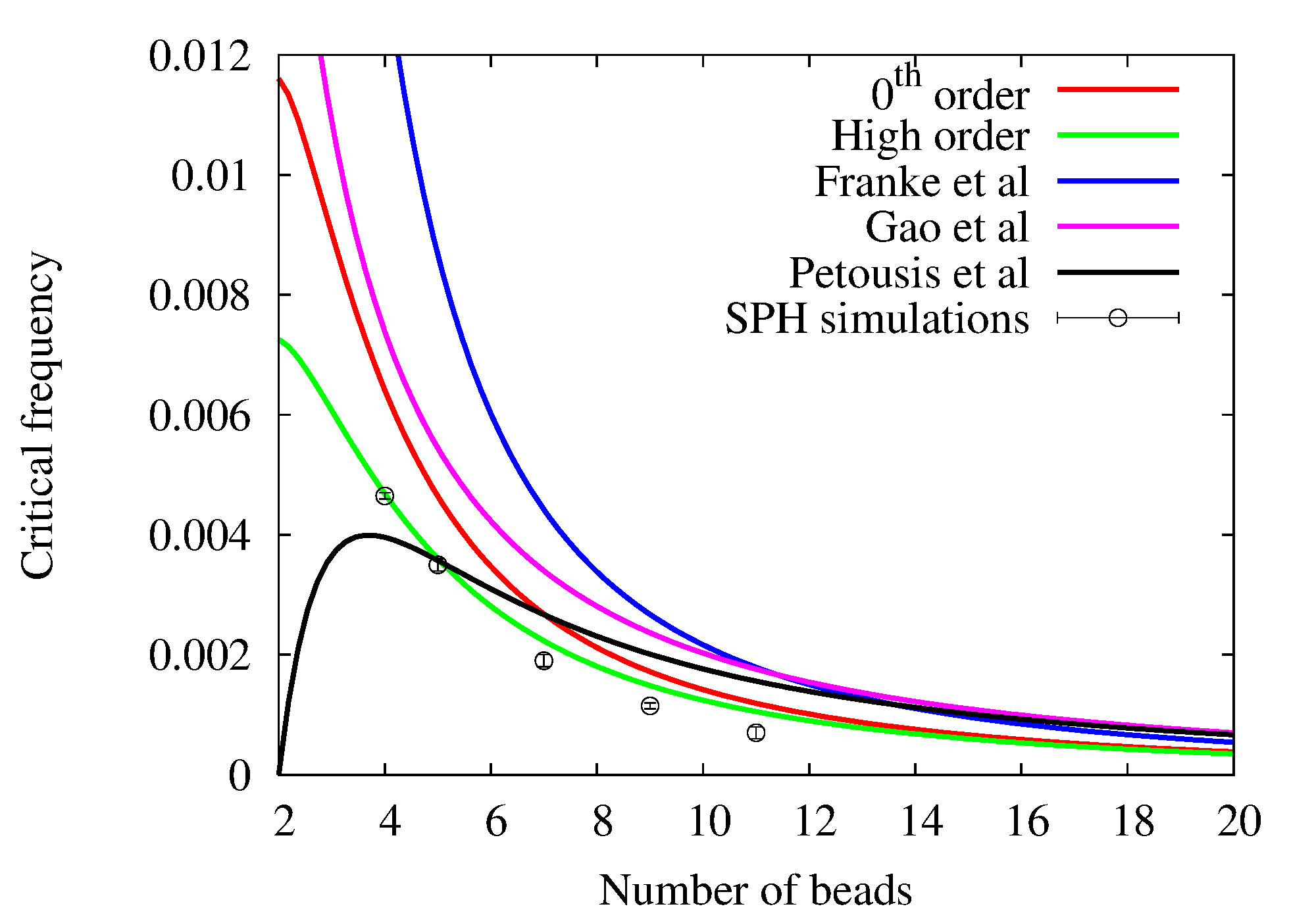

Fig. 8: Critical frequency vs chain size (# beads). Left: theory from [19] compared to literature results and direct numerical simulations using SPH. Right: theory from [19] compared to experimental data.
Recently in [20] we have explored numerically the rheological response of a suspensions of chains of supermagnetic particles under combined effect of shear flow and external actuation using a rotating magnetic field (fig. 9). The suspension viscosity can be controlled (increased or lowered) by tuning the magnetic frequency with the natural shear frequency.
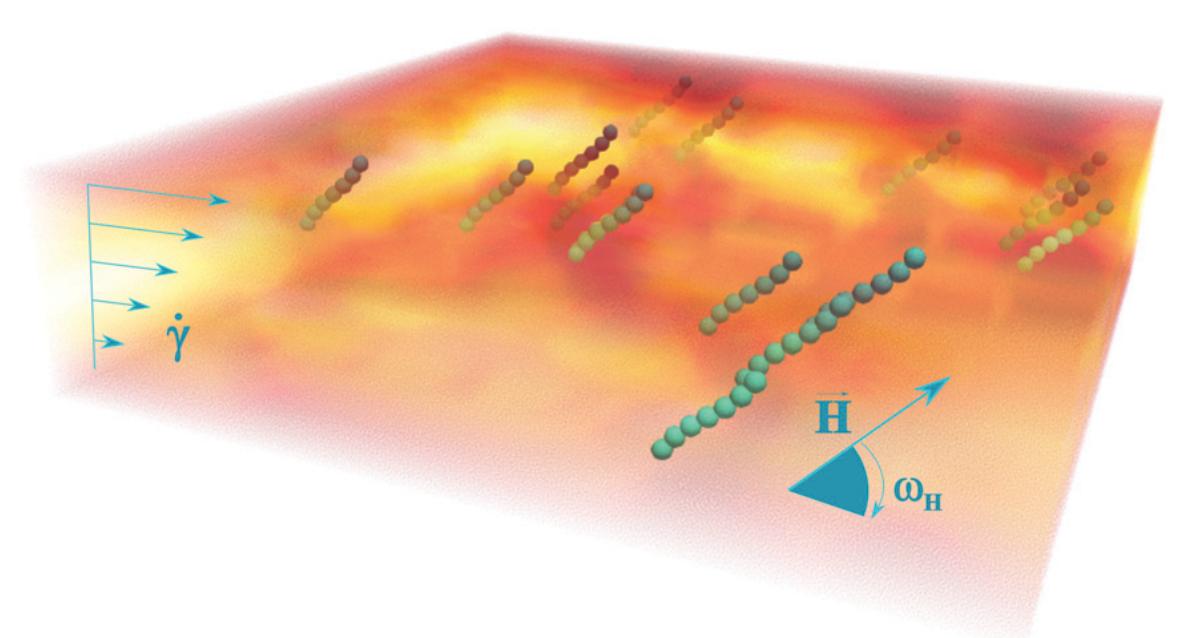
Fig. 9: A suspension of magnetic chains under the effect of an external rotating field and applied shear flow is simulated using SPH.
Arbitrary-shape particles: star-colloids
References
[1] M Ellero, P Español (2018), Everything you always wanted to know about SDPD⋆ (⋆but were afraid to ask),Applied Mathematics and Mechanics 39,103-124 doi
[2] Bian, X., S. Litvinov, R. Qian, M. Ellero, and N. A. Adams (2012). Multiscale modeling of particle in suspension with smoothed dissipative particle dynamics. Physics of Fluids 24(1), 012002. doi
[3] Vazquez-Quesada, A., X. Bian, and M. Ellero (2016). Three-dimensional simulations of dilute and concentrated suspensions using Smoothed Particle Hydrodynamics. Computational Particle Mechanics 3 (2), 167-178. doi
[4] Vazquez-Quesada, A. and M. Ellero (2016). Rheology and microstructure of non-colloidal suspensions under shear studied with smoothed particle hydrodynamics, Journal of Non-Newtonian Fluid Mechanics 233, 37-47. doi
[5] A Vázquez-Quesada, M Ellero (2022), GENERIC-compliant simulations of Brownian multi-particle systems: modeling stochastic lubrication, SeMA Journal, 79, 165–185. doi
[6] A Vázquez-Quesada, M Ellero (2023) , Numerical simulations of Brownian suspensions using Smoothed Dissipative Particle Dynamics: Diffusion, rheology and microstructure, Journal of Non-Newtonian Fluid Mechanics 317, 105044 2023. doi
[7] Vazquez-Quesada, A., M. Ellero, and P. Espanol (2012). A SPH-based particle model for computational microrheology. Microfluidics and Nanofluidics 13 (6), 1 12. doi
[8] Vázquez-Quesada, M Ellero (2017) SPH modeling and simulation of spherical particles interacting in a viscoelastic matrix, Physics of Fluids 29 (12) 121609 doi
[9] A Vázquez-Quesada, P Español, RI Tanner, M Ellero (2019), Shear thickening of a non-colloidal suspension with a viscoelastic matrix, Journal of Fluid Mechanics 880, 1070-1094 doi
[10] Bian, X. and M. Ellero (2014). A splitting integration scheme for SPH simulations of concentrated particle suspensions. Comp. Phys. Comm. 185(1), 53 62. doi
[11] SSP Kumar, A Vázquez-Quesada, M Ellero (2022), A conservative lubrication dynamics method for the simulation of dense non-colloidal suspensions with particle spin, Journal of Computational Physics 427, 110001. doi
[12] Vazquez-Quesada, A., M. Ellero (2016). Analytical solution for the lubrication force between two spheres in a bi-viscous fluid, Physics of Fluids 28 (7), 073101 doi
[13] A Vázquez-Quesada, NJ Wagner, M Ellero , Normal lubrication force between spherical particles immersed in a shear-thickening fluid, Physics of Fluids 30, 123102 (2018) doi
[14] Vazquez-Quesada, A., R.I. Tanner, M. Ellero (2016). Shear Thinning of Noncolloidal Suspensions, Physical Review Letters 117 (10), 108001 doi
[15] Adolfo Vazquez-Quesada, Arif Mahmud, Shao-Cong Dai, Marco Ellero, Roger I. Tanner (2017), “Investigating the Causes of Shear-Thinning in Non-Colloidal Suspensions: experiments and simulations”, J. Non-Newt Fluid Mech. 248, 1-7. doi
[16] A Vázquez-Quesada, P Espanol, M Ellero (2018), Apparent slip mechanism between two spheres based on solvent rheology: Theory and implication for the shear thinning of non-Brownian suspensions Physical Review Fluids 3 (12), 123302 , doi
[17] SSP Kumar, A Vázquez-Quesada, M Ellero (2020) , Numerical investigation of the rheological behavior of a dense particle suspension in a biviscous matrix using a lubrication dynamics method, Journal of Non-Newtonian Fluid Mechanics 281, 104312 doi
[18] JA Ruiz-Lopez, SS Prasanna Kumar, A Vazquez-Quesada, J de Vicente, M Ellero (2023), Tribological variable-friction coefficient models for the simulation of dense suspensions of rough polydisperse particles,, Journal of Rheology 67 (2), 541-558 doi
[19] A Vazquez-Quesada, T Franke, M Ellero (2017), “Theory and simulation of the dynamics, deformation, and breakup of a chain of superparamagnetic beads under a rotating magnetic field” Physics of Fluids 29 (3), 032006 doi
[20] E Rossi, JA Ruiz-Lopez, A Vazquez-Quesada, M Ellero (2021), Dynamics and rheology of a suspension of super-paramagnetic chains under the combined effect of a shear flow and a rotating magnetic field Soft Matter 17 (24), 6006-6019 doi