The increasing technological need to create and manipulate structures on micrometer scales and smaller has triggered the development of many numerical techniques for simulating flow problems at microscales. An emerging area is represented by bio-microfluidics where a single or a collection of molecules are actuated by accurate control of very small amounts of liquid (<ml) flowing through complex micro-devices. A challenging aspect in the modelling of complex fluids on these micro-scales (<<mm) is that no scale separation is present between the size of the suspended microstructure (e.g. the polymer molecule, colloid, cell etc.) and the external device, in such a way that no continuum model based on set of PDEs can be used. Instead, direct modelling of the microstructure, i.e. the dispersed phase, is required.
In our group we have developed a coarse-grained polymer-molecule model (Fig.1 left) where the Brownian solvent is described by the Smoothed Dissipative Particle Dynamics methods (SDPD) [1] which is a “thermodynamic-consistent” mesoscopic particle method for Fluctuating Hydrodynamics [2,3].
Microfluidics-based rheometers
An area of application involved the analysis of a virtual microfluidics-based rheometry (Fig. 1, right), where our mesoscopic simulations have allowed to clarify the link between the spatial flow relaxation of the complex liquid occurring along the channel with the microstructural relaxation processes of the single suspended polymers [4].

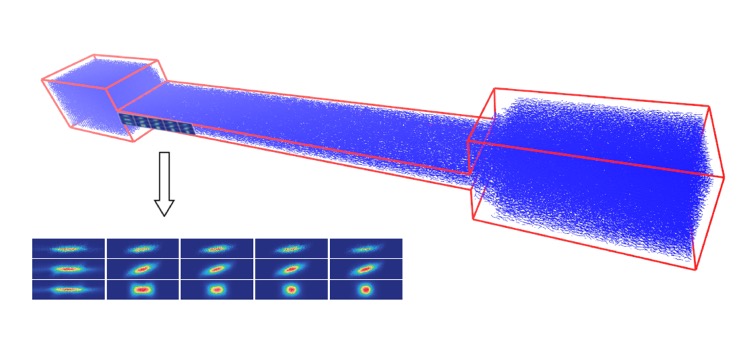
Fig. 1: Left: mesoscopic model of a single polymer molecule suspended in a thermal solvent [1]. Right: microfluidics-based rheometer: a polymeric fluid is injected into the left chamber and undergoes a sudden contraction. Mesoscopic simulations have been carried out to understand the link between microstructure changes and evolution of the macroscopic flow [4].
Inertial polymer drag enhancement and polymer migration
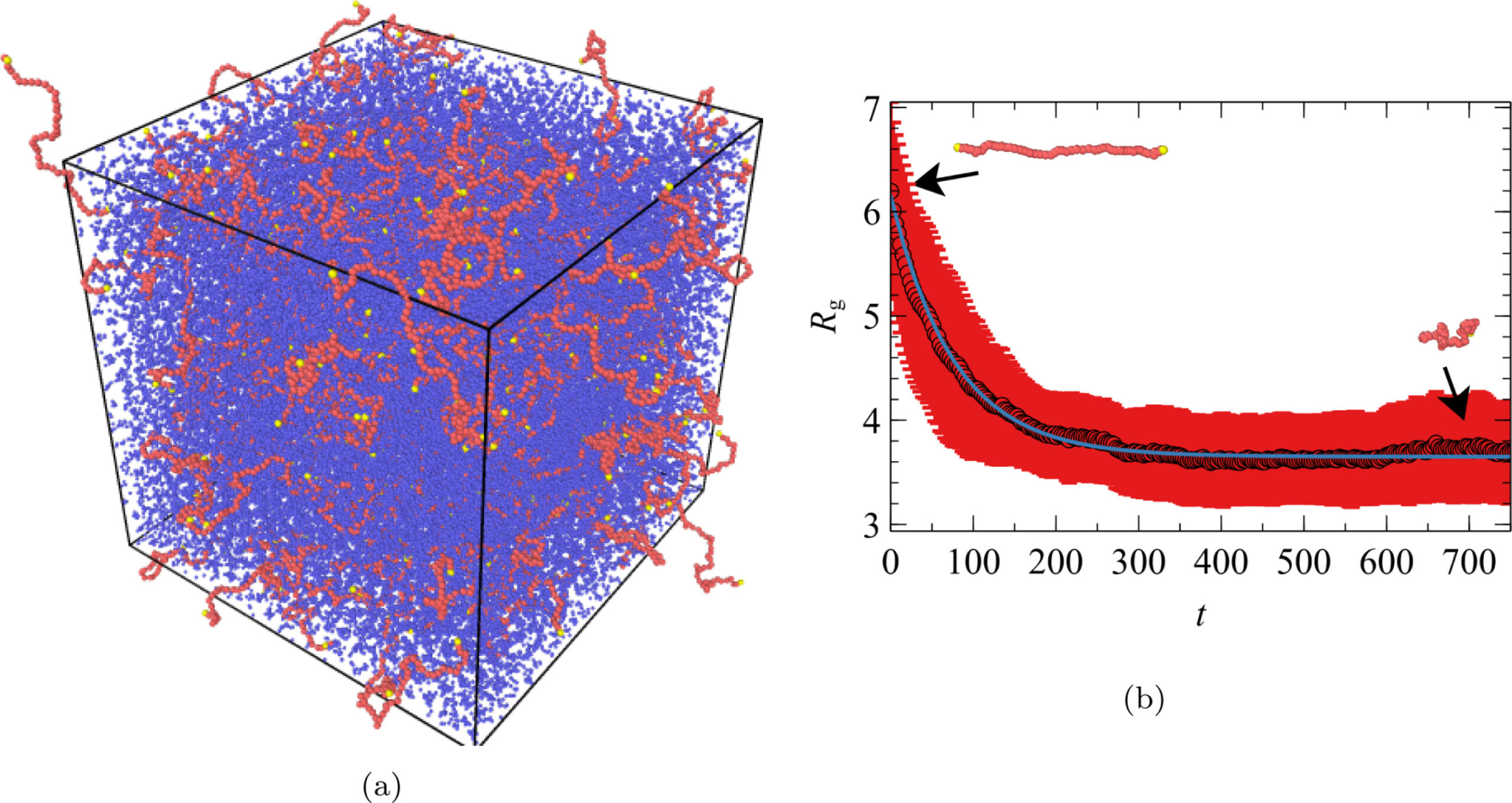
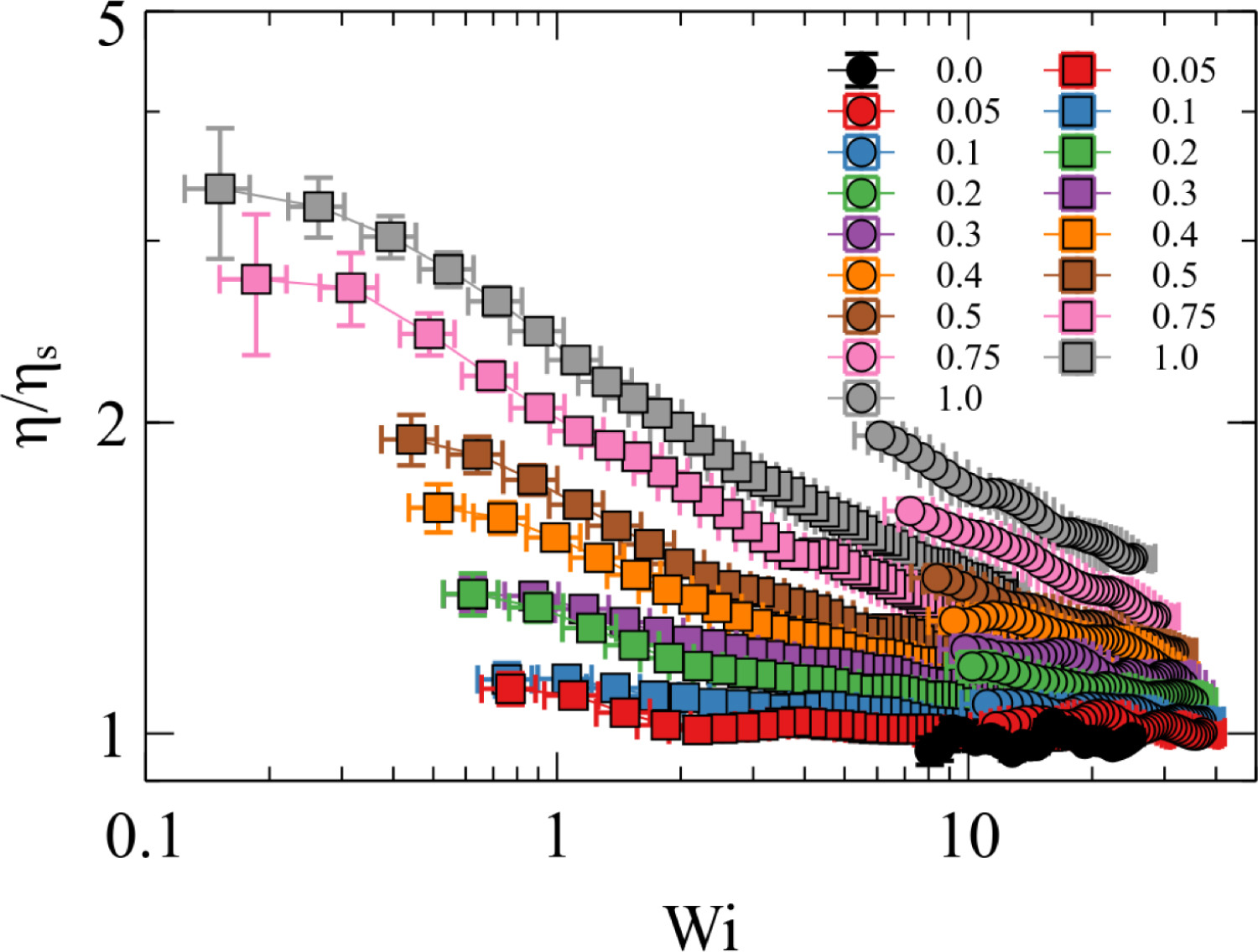
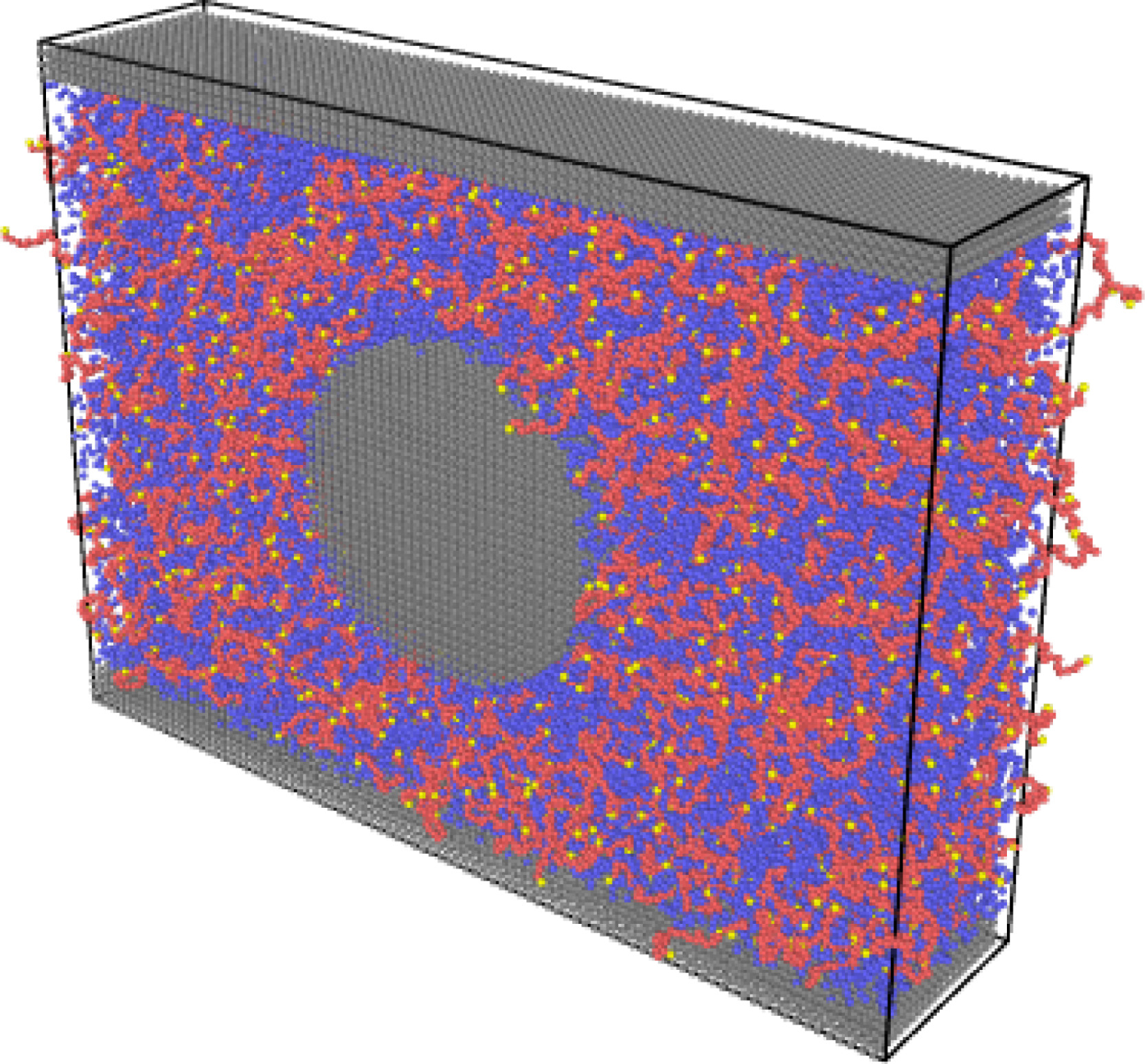
More recently, after full microscopic (Fig. 2: left) and rheological (Fig 2. right) characterisation of the polymer suspension, we have explored the polymer dynamics in complex channel flow with obstacle (Fig 3. left)….

References
[1] S Litvinov, M Ellero, X Hu, NA Adams (2008), Smoothed dissipative particle dynamics model for polymer molecules in suspension Physical Review E 77 (6), 066703. doi
[2] Vázquez-Quesada, M Ellero, P Español (2009), Consistent scaling of thermal fluctuations in smoothed dissipative particle dynamics, J Chemical phys. 130 (3) 034901. doi
[3]M Ellero, P Español (2018) Everything you always wanted to know about SDPD⋆ (⋆but were afraid to ask) Applied Mathematics and Mechanics 39, 103-124 53. doi
[4] S Litvinov, Q Xie, X Hu, N Adams, M Ellero (2016) Simulation of individual polymer chains and polymer solutions with smoothed dissipative particle dynamics Fluids 1 (1), 7. doi
[5] S Litvinov, M Ellero, X Hu, NA Adams (2010), Particle-layering effect in wall-bounded dissipative particle dynamics Physical Review E 82 (6), 066704. doi
[6] S Litvinov, X Hu, M Ellero, N Adams (2014), Mesoscopic simulation of the transient behavior of semi-diluted polymer solution in a microchannel following extensional flow Microfluidics and Nanofluidics 16, 257-264. doi
[7] DN Simavilla, M Ellero (2023), Mesoscopic simulations of inertial drag enhancement and polymer migration in viscoelastic solutions flowing around a confined array of cylinders J. Non-Newtonian Fluid Mechanics 305, 104811. doi
[8] D Nieto Simavilla, P Español, M Ellero (2023) , Non-affine motion and selection of slip coefficient in constitutive modeling of polymeric solutions using a mixed derivative Journal of Rheology 67 (1), 253-267. dog
[9] E Zohravi, N Moreno, M Ellero (2023), Computational mesoscale framework for biological clustering and fractal aggregation Soft Matter 19 (38), 7399-7411. doi
2018 Self-diffusion coefficient in smoothed dissipative particle dynamics S Litvinov, M Ellero, X Hu, NA Adams The Journal of chemical physics 130 (2) 51 2009 A splitting scheme for highly dissipative smoothed particle dynamics S Litvinov, M Ellero, XY Hu, NA Adams Journal of Computational Physics 229 (15), 5457-5464
