The general objective of this research line is the mathematical modelling and related algorithmic development of coupling schemes for complex fluids designed at different spatio-temporal scales. The focus is on two-level micro-macro coupling tools, where “micro” is generally defined in terms of a microstructural mesoscopic model for the complex fluid (i.e. suspended polymers, particles, droplets etc.), whereas ” macro” pertains to the continuum description of conservation equations based on a PDEs framework.
Heterogeneous Multiscale Modelling
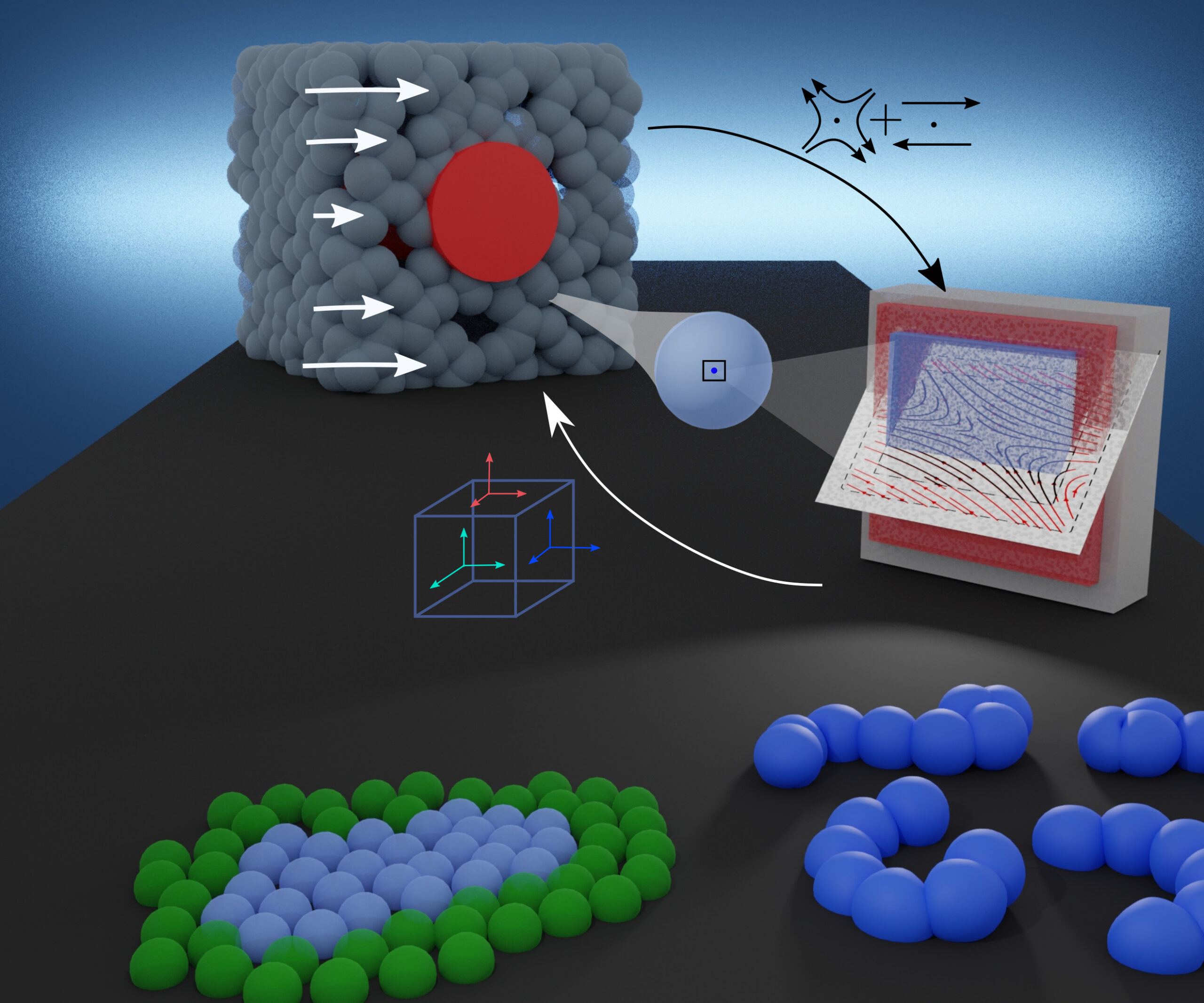
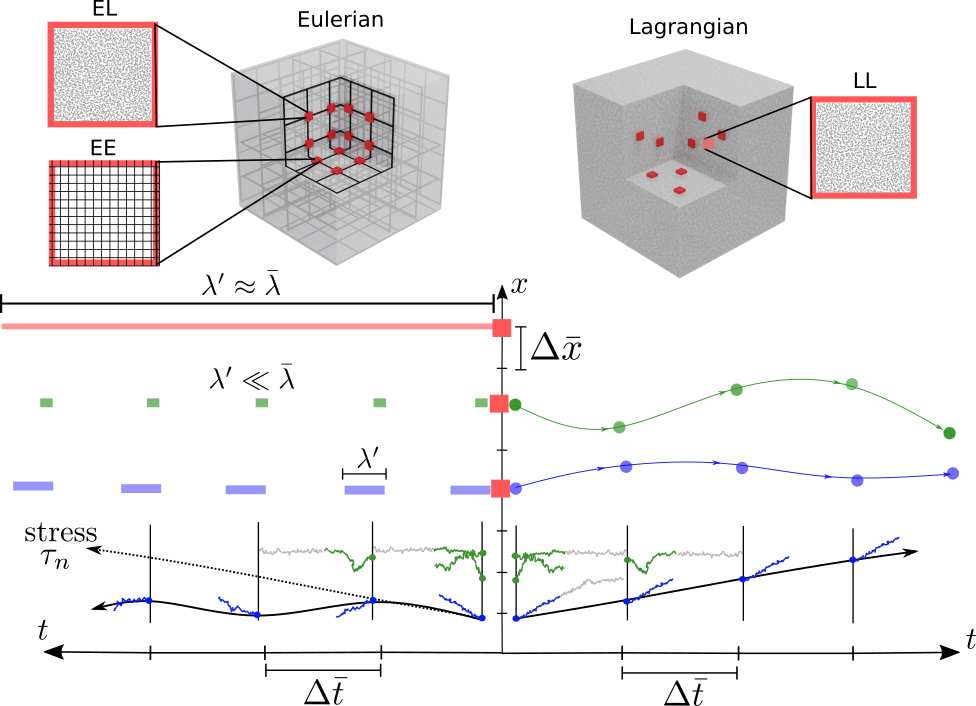
Fig 1: Typical heterogeneous multiscale modelling approaches and time scales features.
Heterogeneous multiscale methods (HMM) that combine numerical algorithms to resolve separately macro and micro-scales, appear as powerful tools to model the behaviour of fluids across scales. In HMMs, microscales are localized and solved on parts of the domain to obtain microscopically-derived properties that are used to close the macroscale problem. This methodology offers the advantage of capturing microscopic effects at the macroscopic length scales, with a lower cost than solving the full microscale problem in the whole domain.
Currently, large part of the existent HMMs rely on Eulerian schemes to resolve the macroscale dynamics, and microscale simulations are associated to grid points, where microscopic properties are derived. This approach is suitable for fluids with microstructural relaxation times sufficiently small compared to the macroscopic ones. However, it cannot be applied to complex fluids with finite memory, where stresses (and microstructure) do heavily depend on flow history and relaxation times are likely to be comparable or largely exceed the macroscopic time step.
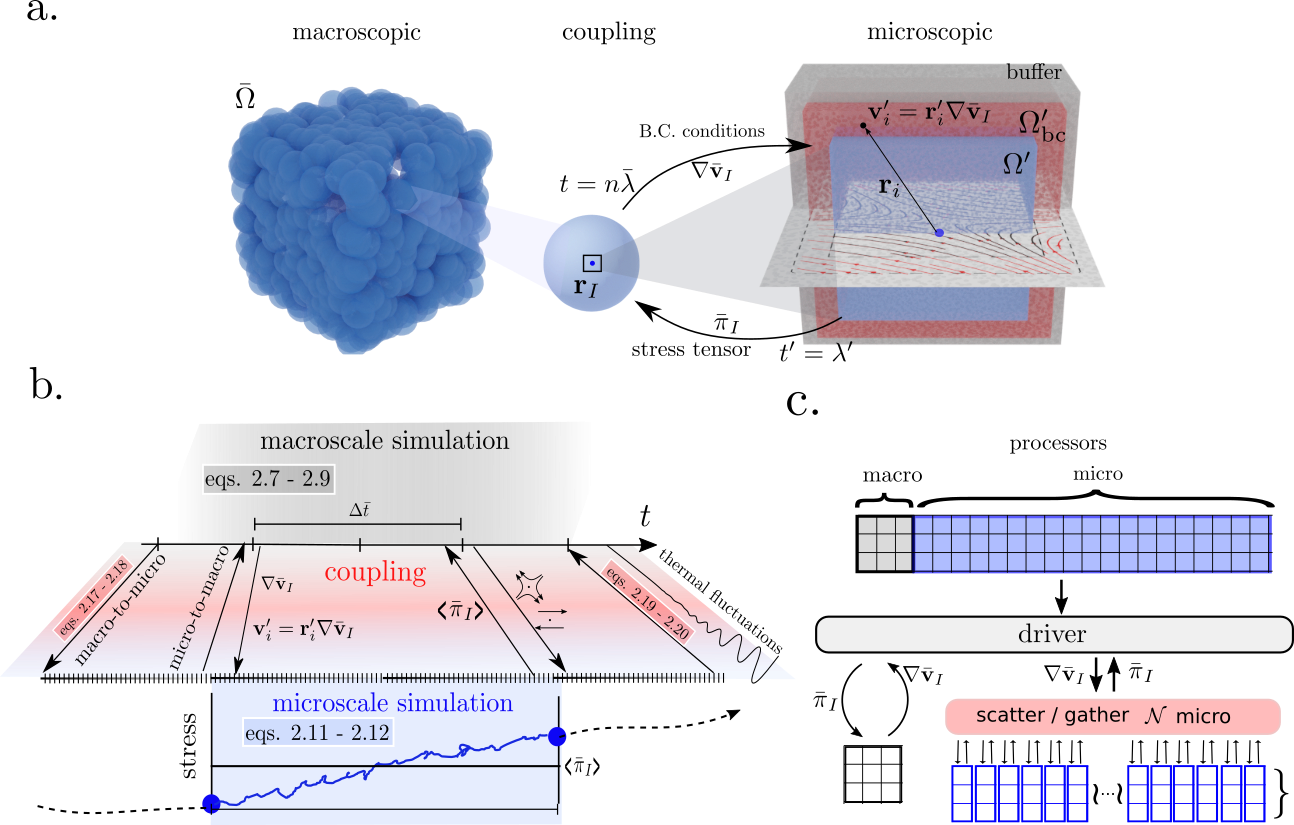
Fig 2: Fully Lagrangian Heterogeneous Multiscale Model Proposed using SDPD [1] and schematic of the macro-micro coupling algorithm. Arbitrary boundary conditions can be seemlesly incorporated using the recently proposed arbitrary boundary conditions model.[4]
We proposed a novel Lagrangian Heterogenous Multiscale Methodology (L-HMM) that discretizises both macro and micro scales using Lagrangian representations [1]. This approach directly track the material points at the macroscale retaining their strain and strain-rate variation, thus naturally handling history-dependent fluids. We adopt the thermodinamically-consistent smoothed dissipative particle dynamics (SDPD) method [2,3] which discretizes the fluctuating Navier-Stokes equations. We have validated the multiscale framework and showcase its flexibility using various flow configurations at the macroscale, and different complex fluids (polymers and multiphase). We demonstrate that our approach is able to capture complex microscopic features on larger scales, altering not only the characteristic steady state conditions of the flow, but also their overall evolution. The practical implementation of the LHMM was done on existent highly paralellizable libraries (LAMMPS) that allowed full parallelization of the method and the flexibility to extend it to a variety of systems.
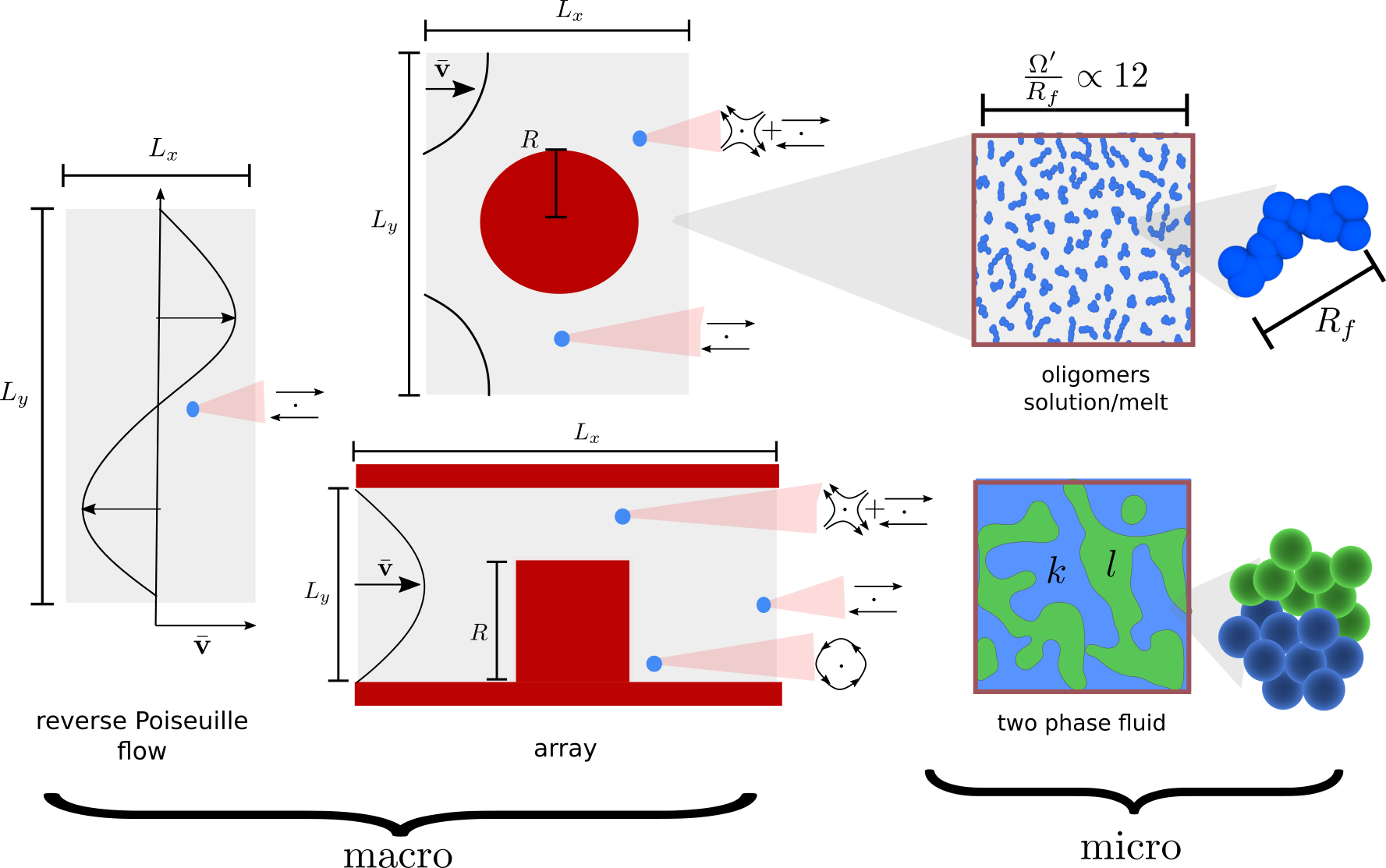
Fig 3: Multiphysics Features of SDPD-LHMM. A variety of complex macroscopic flow can be coupled with a variety of microscopic systems, including polymer solutions, multiphase flows, colloidal suspensions, among others widely modelled at mesoscale using SDPD [3]
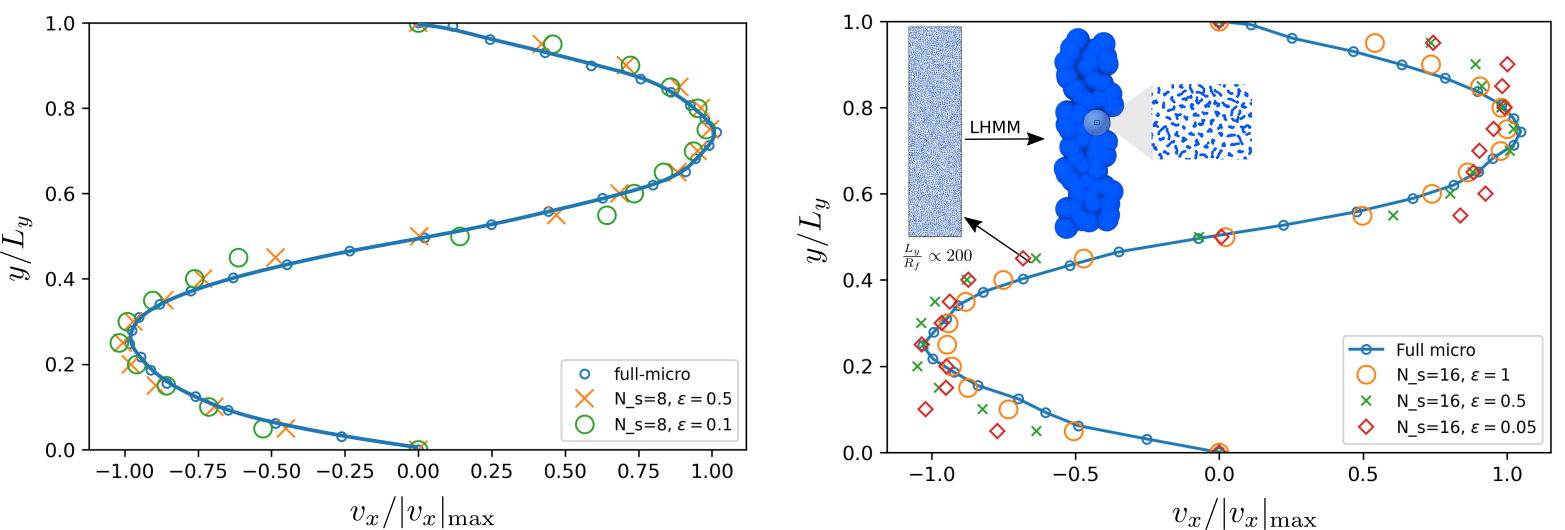
Fig 4: Comparison of fully-microscopically resolved system and LHMM proposed. The variation on the weighting parameter \epsilon, showed that even for LHMM where both ideal and non-ideal effects are accounted from microscales, the model reproduces upto a good approximation the response of the fluid [1]
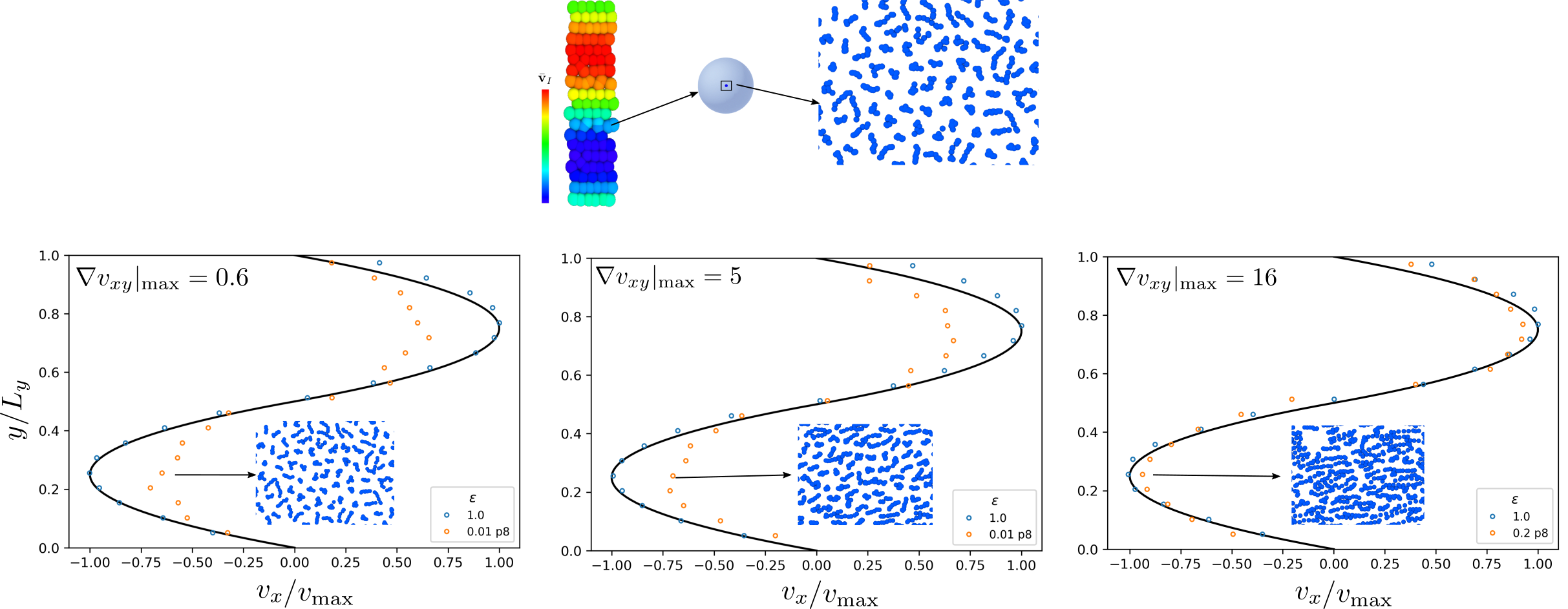
Fig 5: Macroscopic response of polymer solutions. Shear thining behavior steeming from microscopics polymeric solutions give rise alterations in the macroscopic flow.
The proposed methodology has relevance for both computational and theoretical researchers in fluid dynamics of complex fluids ranging from colloidal suspensions, polymer solutions, emulsions, and biological fluids
Arbitrary Boundary Conditions for SDPD
The increased level of sophistication achieved in the design of micro and nanodevices for processing and fluid characterization, go hand in hand with the need for computational methods suitable to model complex flow configurations. One limitation of such computational methods is the definition of non-traditional boundary conditions able to capture the complexity of the flow whereas accounting correctly for fluid properties and near-wall dynamics at microscales. Although methodologies to simulate bulk dynamics in simple flow are well established, arbitrary flows are still challenging or may require not straightforward modifications of the existing codes. We ha recently introduced a novel and simple approach to define boundary conditions that allow the particle simulation of arbitrary flow configurations to study both bulk and near-wall dynamics.
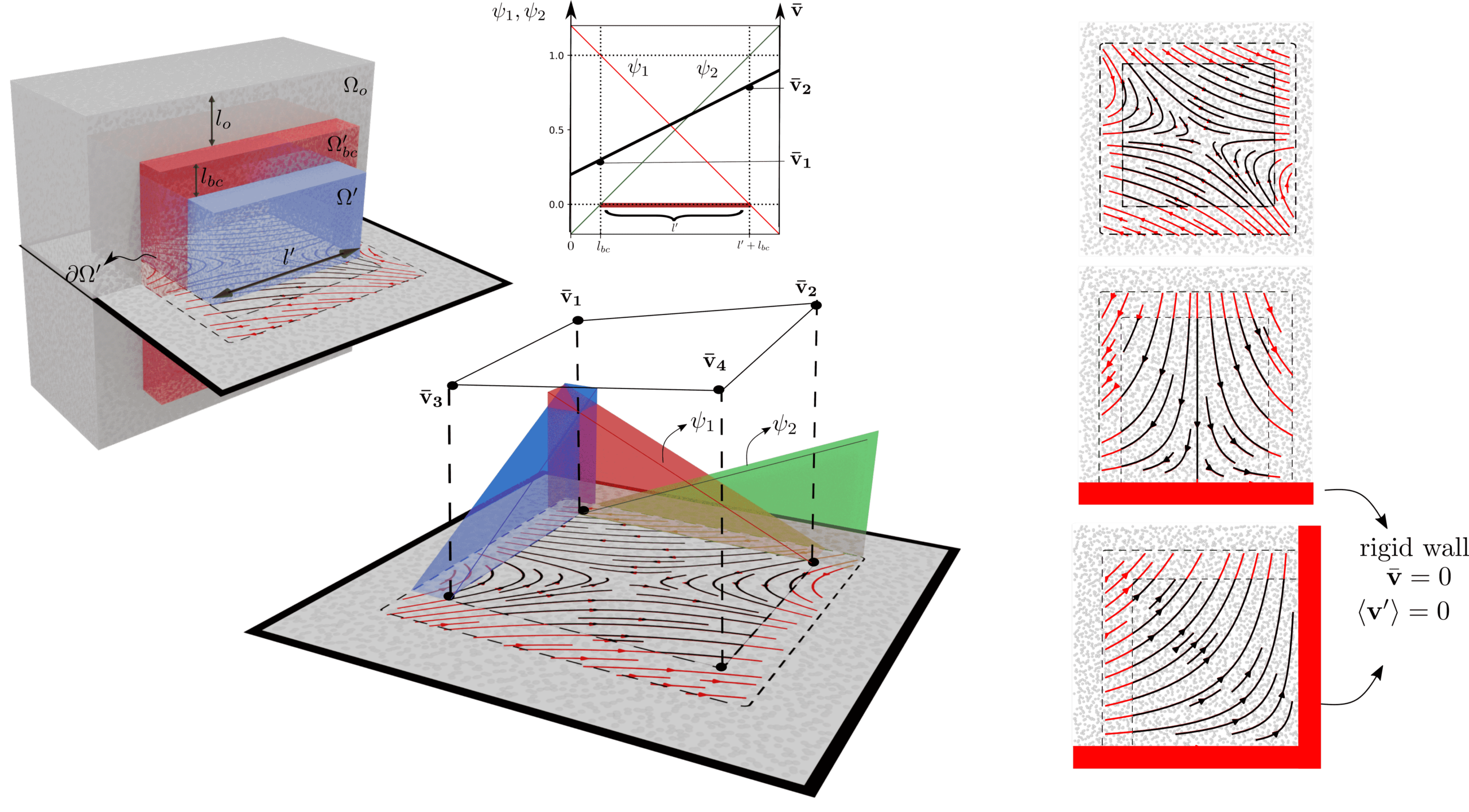
Fig 6: Sketch of the domain decompositions adopted for arbitrary boundary conditions. Velocity interpolation from the prescribed velocity profiles at the boundary condition region allow us to compute the effective stresses at the core region.
We introduce a boundary condition scheme to impose arbitrary velocity fields driving the dynamic response of the system. Our method relies on a domain decomposition approach (see Figure 6) that allows the simulation of mixed flows (shear and extension) using standard periodic-boundary condition and without recurring to explicit deformation of the computational domain. The proposed methodology, along with the smoothed dissipative particle dynamics (SDPD) method [2,3], provides a generalized virtual tool to extract rheological properties of complex fluids. Additionally, since SDPD is a thermodynamically-consistent discretization of the fluctuating Navier-Stokes equations, the introduced methodology is suitable for rheological characterization of systems ranging from continuum to nanoscale. We validate proposed methodology for benchmark problems in simple shear and extensional flow and demonstrate its versatility to model mixed-flow configurations (fig 7) and complex fluids such as polymer solutions [5].
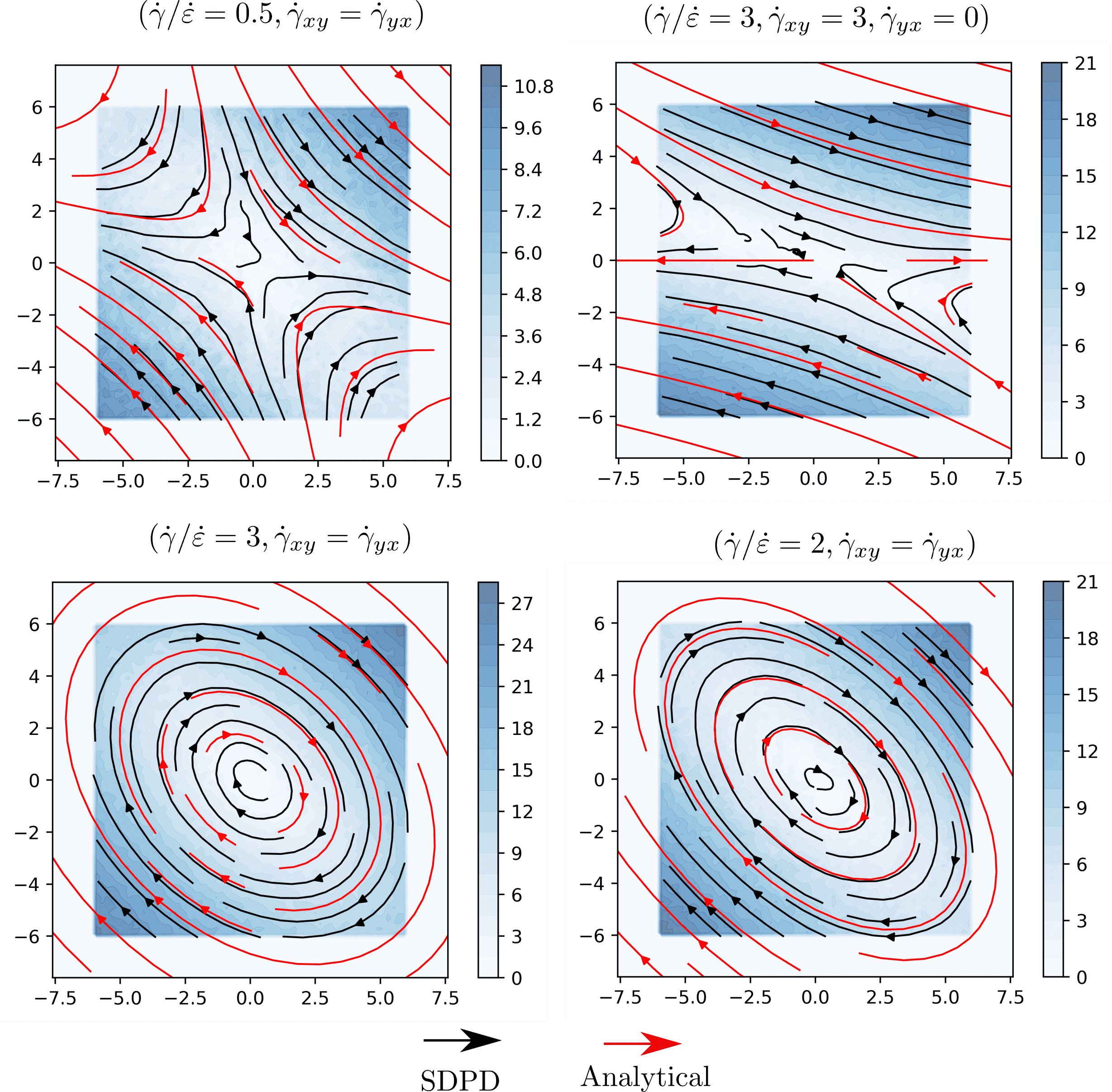

Fig 7: Left: Comparison of the velocity profiles in an arbitrary boundary conditions simulations, for a variety of complex flows. In black, velocity profiles measured vs velocity profiles imposed (at the boundary condition region) in red. Right: heological charaterization of different polymeric solutions. Both shear and normal stresses can be properly recovered.
The L-HMM model has potential applicability in a variety of problems where the rheological characterization requires the modelling complex fluids and flow configurations, such as micro-nano devices, protein dynamics, biological flows, colloidal and particulate systems, to name a few. The proposed boundary conditions also offer novel opportunities for the design of multiscale methods that bypass the requirement of constitutive equations for complex fluids, by coupling velocity gradient information from continuum scales and microscopically derived stresses
References
[1] Moreno Chaparro, N. and M. Ellero (2023). Generalized Lagrangian Heterogenous Multiscale Modeling of Complex Fluids. J. Fluid Mechanics, 969, 25 August 2023. doi
[2] Ellero, M. and P. Espanol (2018). Everything You Always Wanted to Know About S-DPD* (*But Were Afraid to Ask). Applied Mathematics and Mechanics 39 (1), 103–124. doi
[3] A Vázquez-Quesada, M Ellero, P Español (2009), Consistent scaling of thermal fluctuations in smoothed dissipative particle dynamics. J. Chem. Phys. 130 (3) 034901. doi
[4] Moreno Chaparro, N. and M. Ellero (2021). A virtual rheometer for arbitrary flow configurations in mesoscopic Smoothed Dissipative Particle Dynamics simulations. Phys. Fluids 33 (1), 012006. doi
[5] Nieto, D. and M. Ellero (2022). Mesoscopic simulations of inertial drag enhancement and polymer migration in viscoelastic solutions flowing around a confined array of cylinders. J. Non-Newt. Fluid Mech. 305, 104811. doi
