Microswimmers

Microorganisms are present everywhere where life is present, from the deep seas to soils and even our guts. Many of these microorganisms have evolved to swim using different mechanisms adapted to a very viscous, or low Reynolds number, environment. The focus of this research line is to develop numerical methods to simulate these microswimmers and to study their unique physical behaviour specially with a detailed hydrodynamic approach. Together with our collaborators (Aleks Donev, Blaise Delmotte, and Brennan Sprinkle) we have developed a code that allows to simulate microswimmers with active slip, moving parts or under Brownian motion and it is freely available at Software.

Articulated rigid bodies

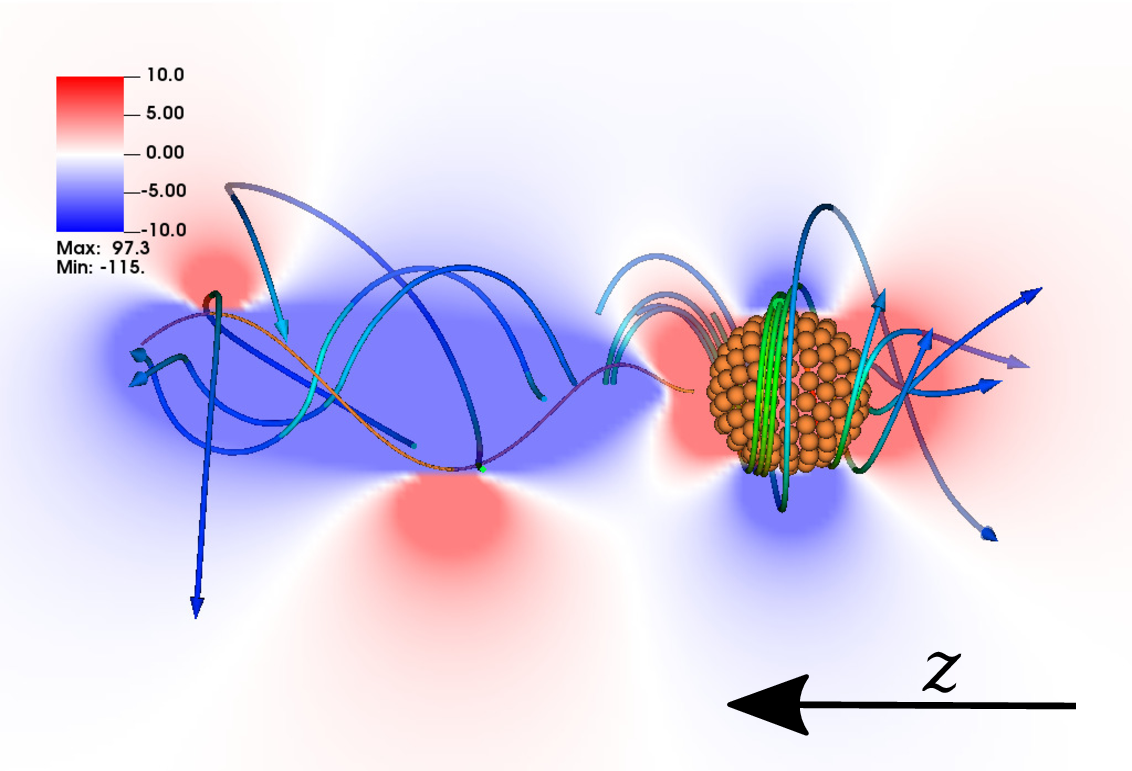
Fig. 1:  Streamlines and magnitude of the velocity (left) and z-vorticity around a bacteria modeled as an articulated rigid body.

An articulated rigid body is a finite number of rigid bodies connected by a set of arbitrary constraints that limit the relative motion between bodies. As microswimmers use moving parts, such as flagella and cilia, to propel within a fluid they can be modeled as articulated rigid bodies. For example, a bacterium can be modeled as a rigid body with an attached rigid flagellum (Fig. 1) and a colony of diatoms can be modeled as set of rods that can slide against each other (Figs. 2 and 3).

We have developed a numerical solver to simulate articulated rigid bodies immersed in a Stokes flow [1]. Our implementation solves the Stokes equations and the constraints connecting the bodies simultaneously using an iterative solver for linear systems (GMRES). The linear solver is quite efficient which allows us to simulate up to hundreds of microswimmers as in the Fig. 4.

Fig. 2.: Microscope view of a colony of diatoms (Bacillaria Paxifiller) and articulated rigid model used to simulate them.

Mapping flagellated swimmers to surface-slip driven swimmers

Fig 5: Sketch representing the scheme to compute the optimum slip. The flow generated by a swimmer A is computed in a surface away from the swimmer represented by a circle. For a swimmer B the optimum slip is computed so the flow generated match that of swimmer A. The error decays with the number of degrees of freedom used to discretize the swimmer B.

Modeling the moving parts of microswimmers is very versatile but computationally expensive. We present an alternative to model them as swimmers with an active slip on their surfaces. The optimum slip to model a specific flagellated swimmer is computed by matching the far field flow generated by the flagellated swimmer, (Figs. 5 and 6).

Fig. 6: Average velocity field magnitude around a flagellated microswimmer, the flow generated by a swimmer slip with active slip and flow difference. The flow difference decays exponentially with the distance to the swimmer.

Swimming efficiently by wrapping

Fig. 7: Bacteria inside a pipe with its flagellum in the extended and wrapped configuration. Here we show a dissected section of the pipe to make the bacteria visible

Our canonical view of a swimming bacteria is that of the E. coli, a bacterium with an ellipsoidal body and a flagella bundle forming on its rear. However, other species use other swimming mechanisms. It has been observed that some single-flagellated bacteria can swim with its flagella extended away from its body (like an E. coli) or wrapped around their bodies (Fig. 7) [2]. In this work we show that the bacterium velocity can be enhanced by the wrapped mode in tight pipes (Fig. 8). This suggest that the wrapped mode present an advantage for some bacteria living in confined environments.

References

[1] F. Balboa Usabiaga, B. Delmotte, A numerical method for suspensions of articulated bodies in viscous flows, Journal of Computational Physics 464 (2022) 111365. doi

[2] H. Gidituri, G. Kabacaoğlu, M. Ellero, F. Balboa Usabiaga, Mapping flagellated swimmers to surface-slip driven swimmers, arXiv (2022) arXiv:2302.05121 doi

[3] M. J. Kühn, F. K. Schmidt, B. Eckhardt, K. M. Thormann, Bacteria exploit a polymorphic instability of the flagellar filament to escape from traps, Proceedings of the National Academy of Sciences 114 (24) (2017) 6340–6345.

[4] H. Gidituri, M. Ellero, F. Balboa Usabiaga, Swimming efficiently by wrapping, arXiv (2023) arXiv:2307.04243 doi .