The focus of this research line is on computational fluid dynamics (CFD) with a specialization in non-Newtonian fluids. We employ modeling techniques at the continuum level, utilizing grid-based or Lagrangian particles discretization to solve partial differential equations (PDE) for complex fluids. This encompasses a spectrum of behaviors such as viscoelasticity, thixotropy, plasticity, shear-thinning, and shear-thickening, commonly observed in polymer suspensions, colloidal particle suspensions, elastic networks, and gels. The general objective is to devise precise and efficient CFD models for macro-scale flow simulation of these complex systems, grounded in a continuum mathematical framework.
Elastic turbulence
The continuum flow of polymeric liquids through complex geometries is of paramount importance in many areas of engineering such as composite-polymer manufacturing, extrusion processes, lubrication, enhanced oil recovery etc. In most of these processes the appearance of non-linear instabilities of the complex fluid might affect drastically the dynamics, eventually leading to a chaotic unsteady states even in the absence of fluid inertia (zero Reynolds number): a phenomenon denoted as “elastic turbulence”. Despite the large technological importance of the problem, the flow of highly elastic liquids through complex geometries remains controversial. The main issue is related to a typical sudden large increase in the flow resistance and unsteadiness which is hard to predict properly.
In our group a Lagrangian meshless particle framework for the CFD of viscoelastic fluids based on the Smoothed Particle Hydrodynamics methods (SPH) has been developed in the past decade for differential models [1,2,3] and, more recently, integral models [11].
SPH computations of viscoelastic liquids through a periodic array of cylinders (PAC) have provided evidence of unsteady elastic behavior and enhanced resistance[4], in quantitative agreement with experimental observations and theoretical predictions of the energy spectrum [5]. Simulations under PAC indicate that for a sufficiently large level of fluid elasticity, a chaotic self-sustained state corresponding to inhomogeneous near-wall structures of polymer over/under-extension (Fig. 1, top/left) can be established where enhanced mixing of mass takes place (Fig.1, bottom/left) and power-law decay of the energy spectrum is observed (Fig. 1 right) [5]. The objective of this research direction is, on one hand, to understand the origins of these flow instabilities and, on the other, to explore novel strategies to control micro-mixing based on elastic turbulence.
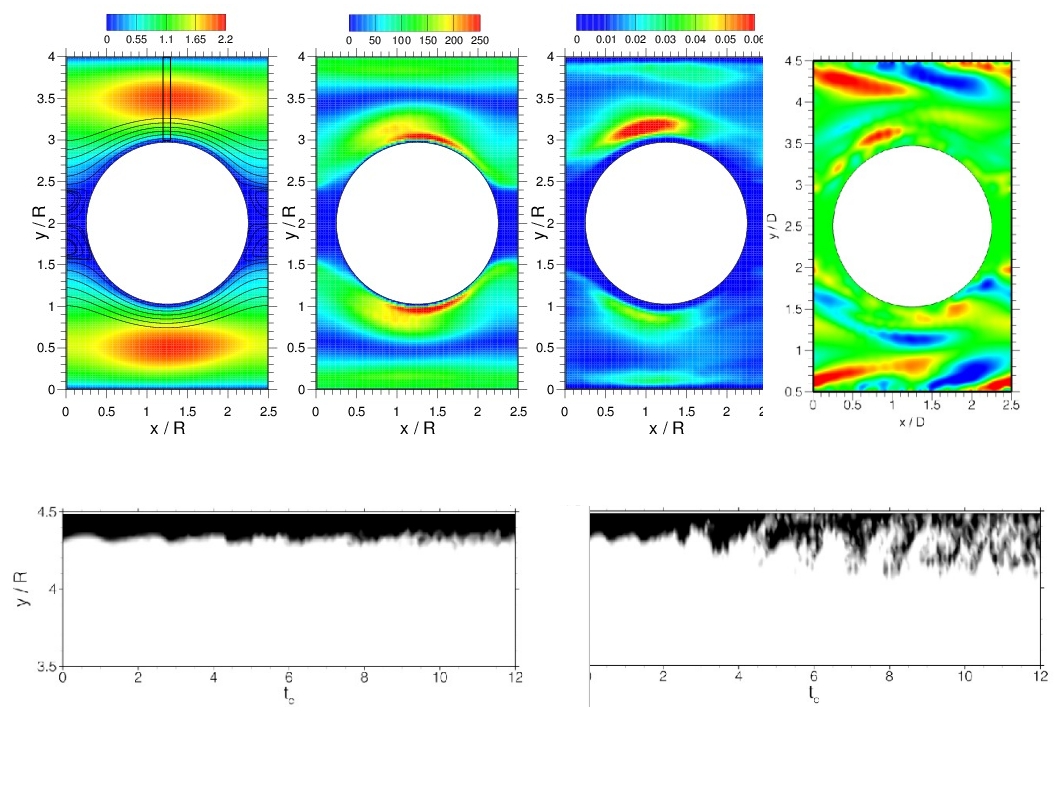
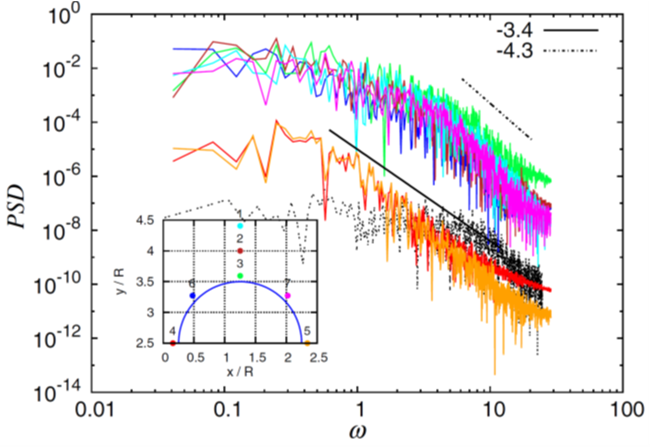
Fig. 1: Viscoelastic flow through a periodic array of clinders. Left-Top: a) steady mean velocity field (streamwise direction x); b) steady mean polymer conformation tensor (xx); c) Reynolds stress (xx); d) snapshot main unsteady mode conformation tensor (xx) obtained via Dynamic Mode Decomposition (DMD) analysis. Left-Bottom: space-time diagram of mass mixing in the top near-wall layer with no elastic instability (left) and with instability (right). Right: Power spectrum density velocity fluctuations for no elastic instability (black line) vs elastic instability (colours). [5].
Thixo-viscoplastic fluids
Thixotropic materials are complex fluids that display time-dependent viscosity and/or yield-stress response upon the application of a fixed deformation, while recovering their original structured-state when the deformation is discontinued. We simulate the rheological properties of thixo-viscoplastic flows using a novel Smoothed Particle Hydrodynamic (SPH) method. SPH solutions are compared with simulations performed using the open-source Finite Volume Method solver RheoTool, based on OpenFOAM. The viscoplastic model used in this work is the Papanastasiou model combined with a recently developed transient microstructural model to include thixotropy [7].
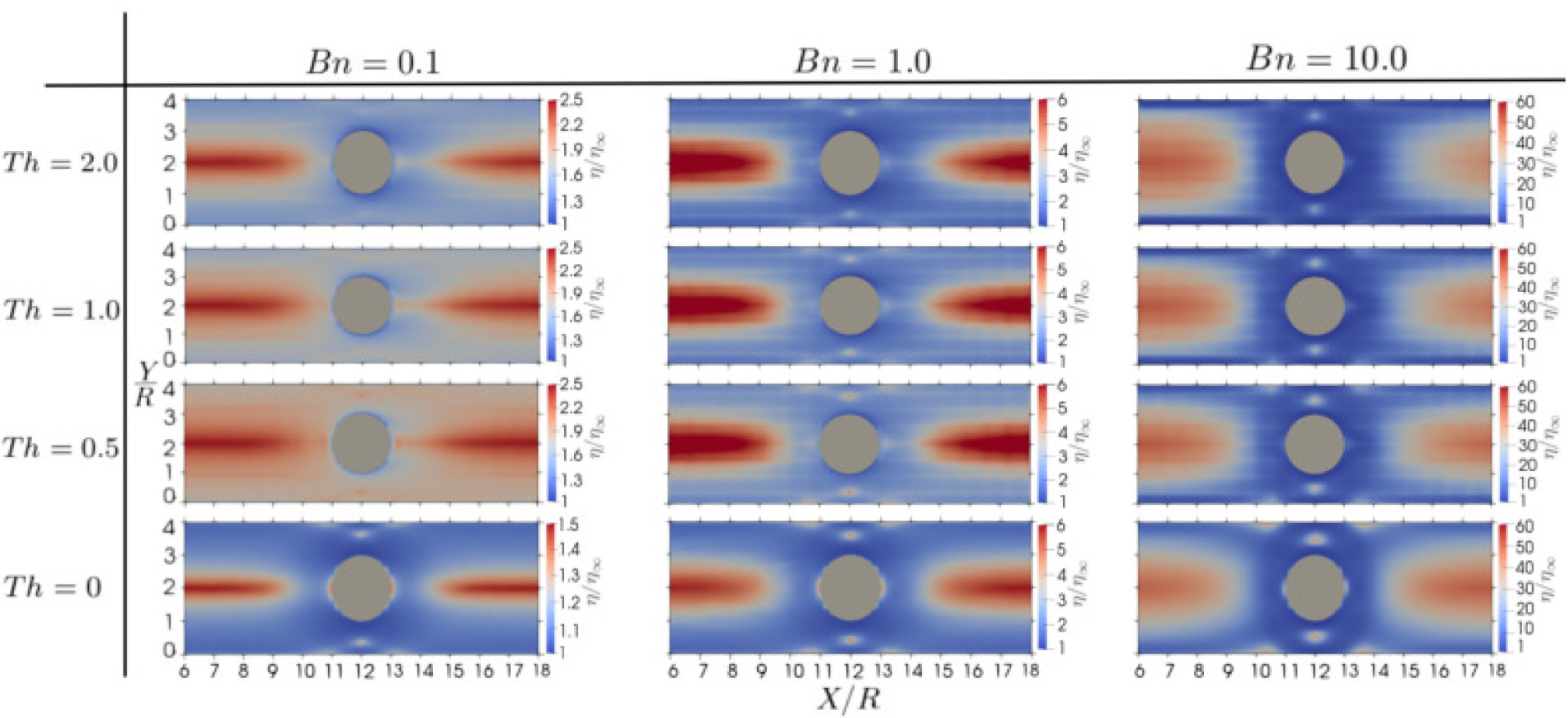
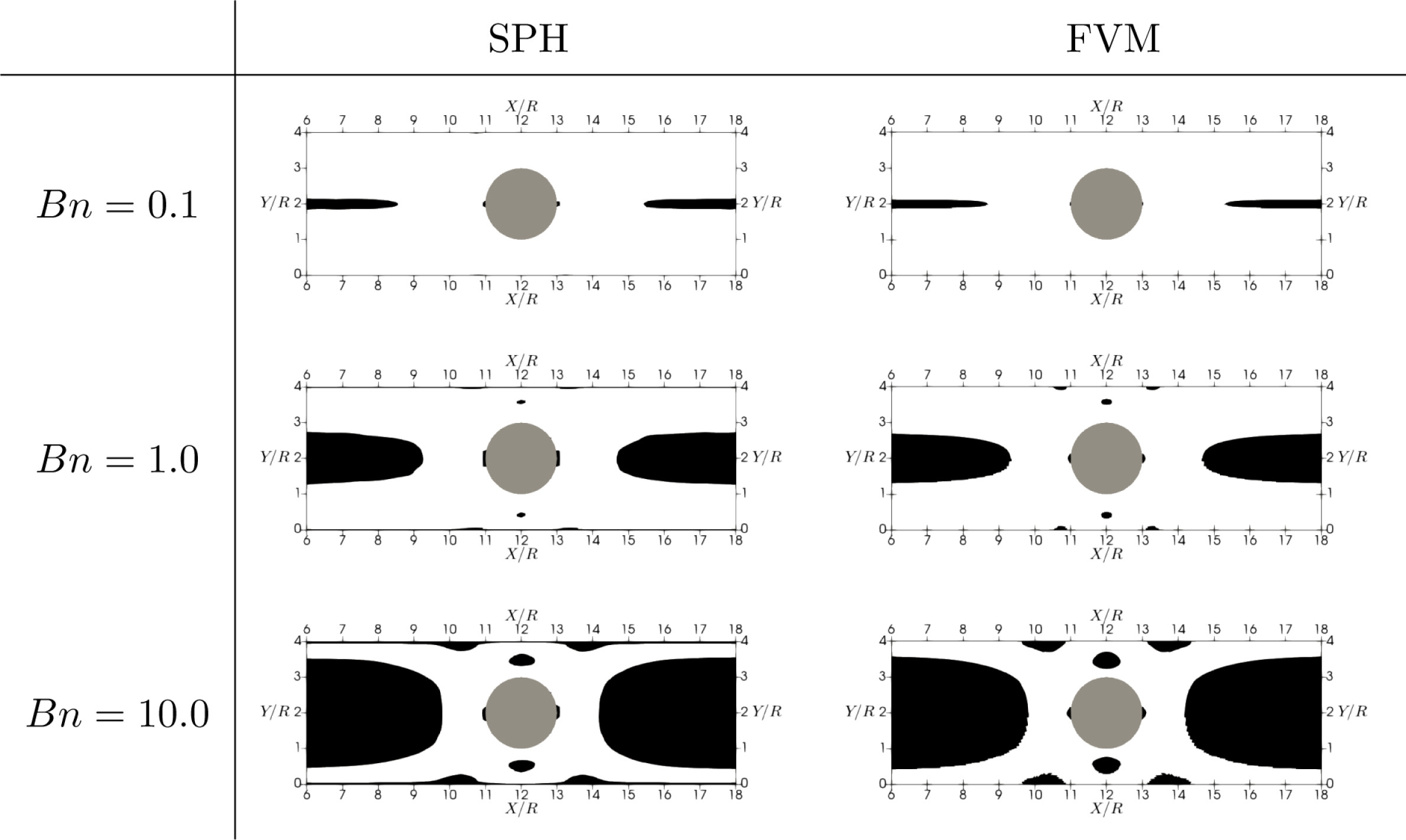
Fig. 2. SPH thixo-viscoplastic model: flow around a cylinder. Left: non-Newtonian viscosity for different dimensionless Thixotropy and Bingham numbers. Right: Comparison of yielded stress regions for SPH vs FVM-based Rheotool at different Bingham numbers [7].
Discontinuous shear-thickening fluids
Some dense suspensions of fine non-Brownian particles can exhibit discontinuous shear thickening (DST) behaviour, a sudden dramatic viscosity increase in response to sufficiently high shear-rates/stress applied to the sample. A defining feature of DST, as opposed to continuous shear-thickening (CST), is the characteristic ‘S’ shape of the flow curve. This unique non-monotonic shape facilitates unstable behaviours in rheometric and complex flows. Recently, we have developed the first implementation of a continuum scalar non-local microstructural DST model (of the Wyart-Cates type) in an SPH scheme. Unlike previous models, we reproduce the challenging S-shaped DST rheology in stress-controlled simple shear experiments as well as characteristically inflexed velocity profiles accompanied by flow reduction behaviour in channel flows [9].
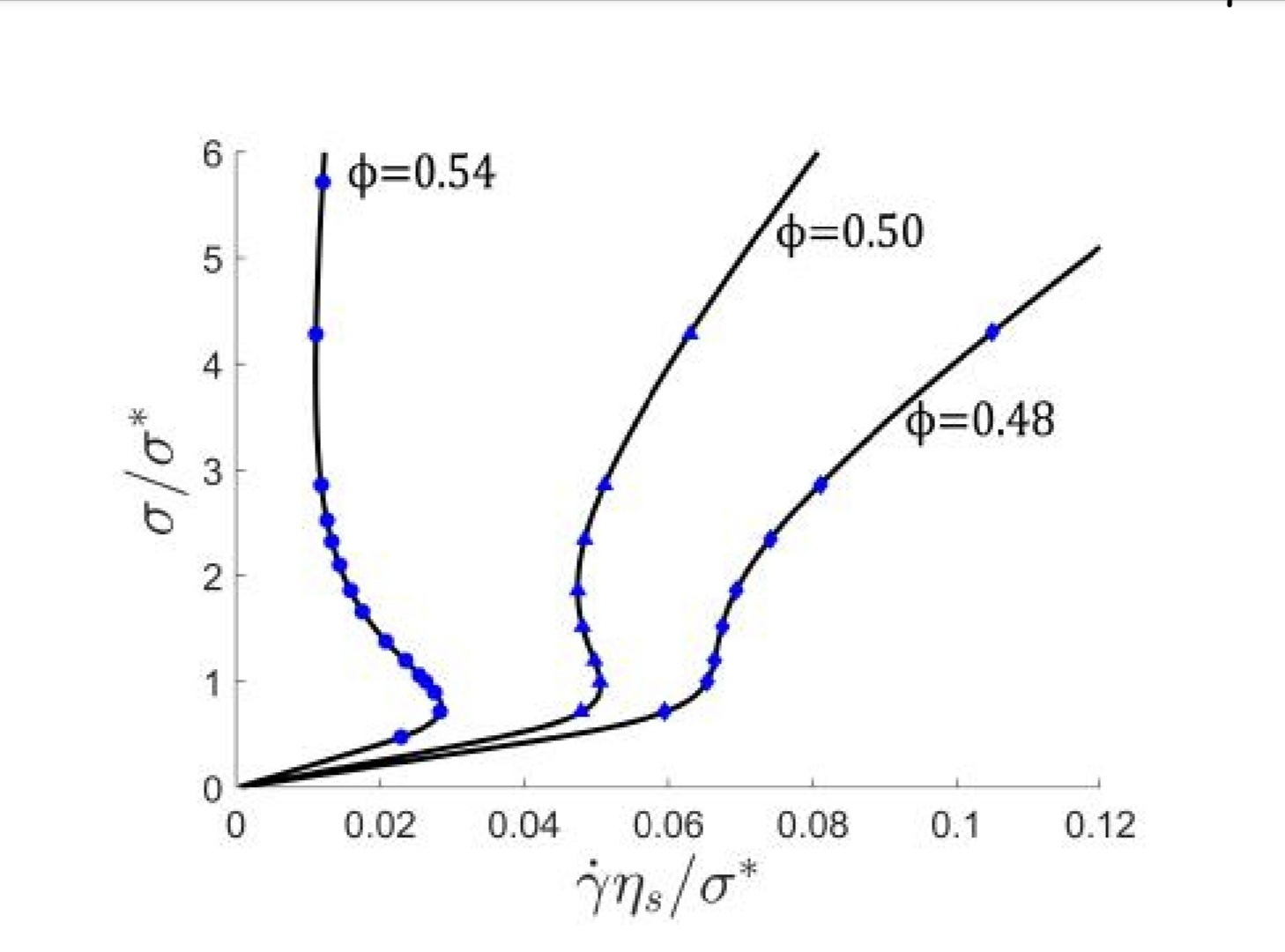
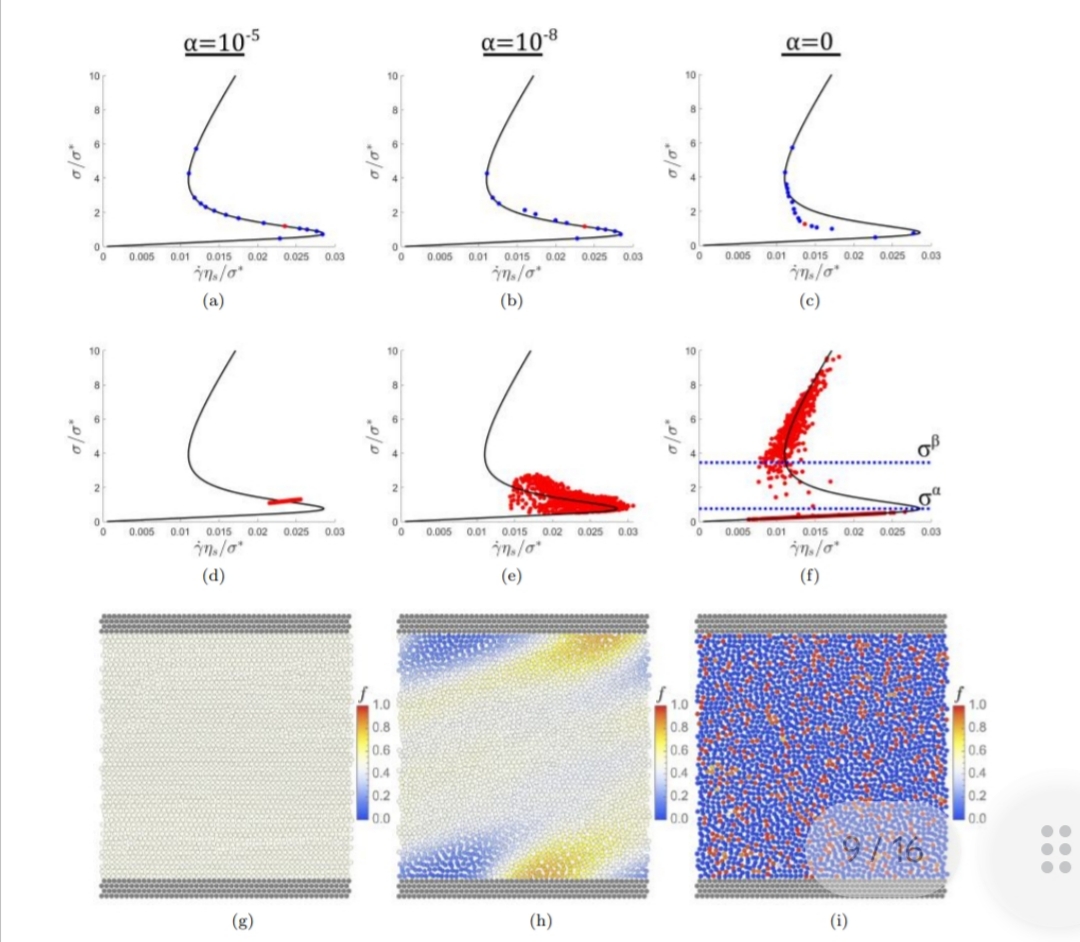
Fig. 4. Wyart-Cates model of the DST fluids: Left: Flow curves in the stress-shear plane at different solid volume fractions. Typical S-shape is accurately obtained by SPH simulations (blue dots). Different S-shape rheologies for different degrees of model non-locality (microstructure diffusion parameter) and corresponding microstructure f-field: homogeneous, heterogeneous, discontinuous (bottom) [9].
Semi-solid molten alloys and liquid metals
The flow patterns of semi-solid aluminium alloys can be studied using the Bautista-Manero-Puig (BMP) model. This model- implemented in a Finite Volumes-based OpenFoam Rheotool package, captures the thixo-viscoelastic behavior of the alloys, specifically at temperatures near their melting point [10]. Notably, thixotropy is a time-dependent change in viscosity, indicating that under certain conditions, a fluid undergoes a transition from a thick, solid-like state to a thinner fluid-like state. While earlier numerical models tried to capture steady non-Newtonian effects, they largely fell short because of their time-independent nature.
The BMP model incorporates time-dependent thixotropic features via a fluidity structure equation. In this approach, the creation and destruction dynamics of the material’s structure are modulated by specific timescales and stress levels. The BMP model has previously been tested in complex flow scenarios [8], making it a valuable tool for analysing the unique properties of aluminium alloys. In particular, when processing aluminium alloys at temperatures close to their melting points, these thixo-viscoelastic properties are critical. Figure 5 shows some results of the study of an open-rotor mixer in terms of viscoelastic effects, which provide valuable insights into how molten alloys can effectively shear and mix under high-shear processing conditions [10].

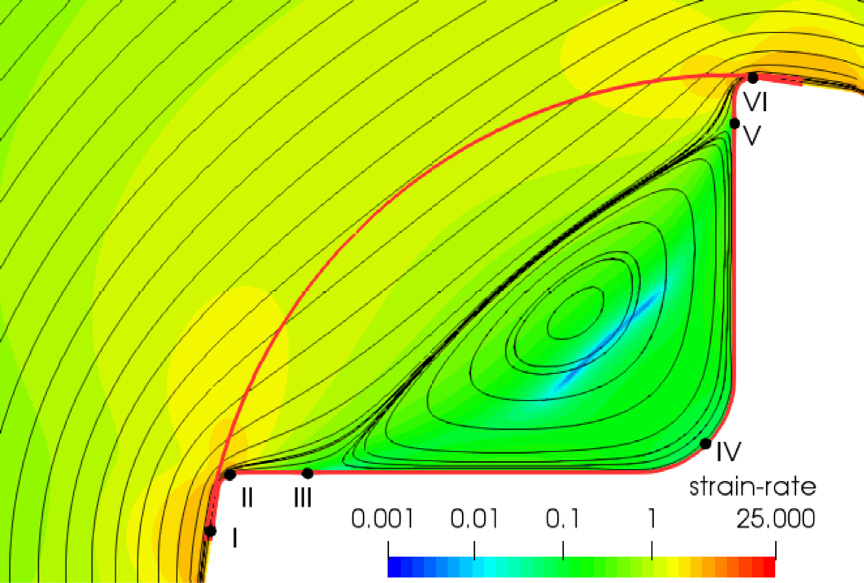

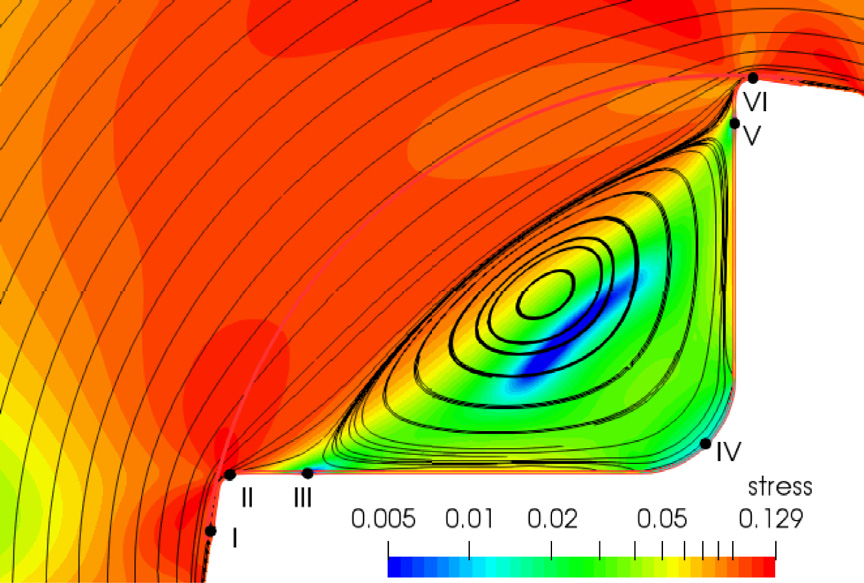
Fig. 5. Top: 3D details of an open-rotor mixer. Bottom: near-blades flow features in the 2D rotor plane. Left: strain-rate; Center: fluidity; Right: stress fields at 60rpm [10].
References
[1] M Ellero, M Kröger, S Hess (2002), Viscoelastic flows studied by smoothed particle dynamics, Journal of Non-Newtonian Fluid Mechanics 105 (1), 35-51. doi.
[2] M Ellero, P Espanol, EG Flekkøy (2003) Thermodynamically consistent fluid particle model for viscoelastic flows , Physical Review E 68 (4), 041504. doi
[3] Ellero, M. and R. Tanner (2005). SPH simulations of transient viscoelastic flows at low Reynolds number. Journal of Non-Newtonian Fluid Mechanics 132(13), 61 –72. doi
[4] A Vázquez-Quesada, M Ellero, P Español (2009), Smoothed particle hydrodynamic model for viscoelastic fluids with thermal fluctuations Physical Review E 79 (5), 056707. doi
[5] A Vázquez-Quesada, M Ellero (2012), SPH simulations of a viscoelastic flow around a periodic array of cylinders confined in a channel Journal of Non-Newtonian Fluid Mechanics 167, 1-8. doi
[6] Grilli, M., A. Vazquez-Quesada, and M. Ellero (2013). Transition to Elastic Turbulence and Mixing in a Periodic Channel Flow. Phys. Rev. Lett. 110, 174501(5). doi.
[7] E Rossi, IG de Beristain, A Vazquez-Quesada, JE López-Aguilar, M Ellero (2022), SPH simulations of thixo-viscoplastic fluid flow past a cylinder Journal of Non-Newtonian Fluid Mechanics 308, 104891. doi
[8] E Lopez-Aguilar, O Resendiz-Tolentino, HR Tamaddon-Jahromi,M Ellero, O Manero (2022), Flow past a sphere: Numerical predictions of thixo-viscoelastoplastic wormlike micellar solutions J, Journal of Non-Newtonian Fluid Mechanics 309, 104902. doi
[9] P Angerman, SS Prasanna-Kuymar, B Sandnes, R Seto, M Ellero (2024), Microstructural SPH Model and Simulations of Discontinuous Shear-Thickening Fluids, Phys. Fluids (in press). doi
[10] I Garcia-Beristain, M Figueroa-Landeta, JE López-Aguilar, MG de Cortazar, F. Girot, M. Ellero (2023), Numerical simulations of thixotropic semi-solid aluminium alloys in open-rotor and rotor-stator mixers Journal of Non-Newtonian Fluid Mechanics, 321, 105128. doi
[11] L. Santelli, A. Vazquez-Quesada, M. Ellero (2023), Smoothed Particle Hydrodynamics model for integral multimodes and fractional viscoelasticity, Journal of Non-Newtonian Fluid Mechanics, under submission.
